Question

【题目】已知函数g（x）=x2﹣（2a+1）x+alnx （Ⅰ） 当a=1时，求函数g（x）的单调增区间；
（Ⅱ） 求函数g（x）在区间[1，e]上的最小值；
（Ⅲ） 在（Ⅰ）的条件下，设f（x）=g（x）+4x﹣x2﹣2lnx，
证明： ＞ （n≥2）．（参考数据：ln2≈0.6931）

Answer 1

【答案】解：（Ⅰ）当a=1时，g（x）=x2﹣3x+lnx， ∴ ，
解得x＞1或x＜ ．
∴函数f（x）的单调增区间为（0， ），（1，+∞）．
（Ⅱ）解：g（x）=x2﹣（2a+1）x+alnx，

=
= =0，
当a≤1，x∈[1，e]，g′（x）＞0，g（x）单调增．g（x）min=﹣2a，
当1＜a＜e，x∈（1，a），g′（x）＜0，g（x）单调减．
x∈（a，e），g′（x）＞0，g（x）单调增．
g（x）min=g（a）=﹣a2﹣a+alna，
当a≥e，x∈[1，e]，g′（x）≤0，g（x）单调减，
g（x）min=e2﹣（2a+1）e+a．
∴g（x）min= ．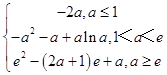
（Ⅲ）证明：令h（x）=lnx﹣ ，
∵x∈[2，+∞）， ，
∴ ，即lnx＜ ，
∴ =2（ ），
k﹣f（k）=lnk，
= =
＞2（1﹣ + ﹣ +…+ ）
＞2（1+ ）
= ，（n≥2）．
∴ ＞ （n≥2）
【解析】（Ⅰ）由 ，能求出函数f（x）的单调增区间．（Ⅱ） = =0，由此根据a的取值范围分类讨论，能求出g（x）min ． （Ⅲ）证明：令h（x）=lnx﹣ ，由x∈[2，+∞），得 ，从而得到 ＞2（ ），k﹣f（k）=lnk，由此能证明 ＞ （n≥2）．
【考点精析】认真审题，首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减)，还要掌握函数的最大(小)值与导数(求函数在上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值，比较，其中最大的是一个最大值，最小的是最小值)的相关知识才是答题的关键．