题目内容
【题目】如图，P—ABCD是正四棱锥，
是正方体，其中
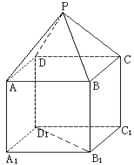
（1）求证：
；
（2）求平面PAD与平面
所成的锐二面角
的余弦值；
【答案】（1）证明见解析（2）
．
【解析】
本试题主要是考查了线面垂直定理和二面角的平面角的求解的综合运用．
（1）建立空间直角坐标系，然后利用点的坐标得到向量的坐标，运用数量积为零证明垂直的问题．
（2）再运用向量的夹角公式表示二面角的平面角的求解的
（理）解：以
为
轴，
为
轴，
为
轴建立空间直角坐标系
（1）证明:设E是BD的中点，
P—ABCD是正四棱锥，
∴
又
， ∴
∴
∴
∴
， 即
.-----------------5分
（2）解:设平面PAD的法向量是
，
∴
取
得
，
又平面
的法向量是
∴
， ∴
.-----------------10分
练习册系列答案
53天天练系列答案
相关题目
【题目】下列说法：
①将一组数据中的每个数据都加上或减去同一个常数后，方差恒不变；
②设有一个回归方程
，变量x增加一个单位时，y平均增加5个单位；
③线性回归方程
必过（
）；
④在一个2×2列联中，由计算得
则有99%的把握确认这两个变量间有关系；
` 其中错误的个数是 （ ）
本题可以参考独立性检验临界值表：
| 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.535 | 7.879 | 10.828 |
A.0B.1C.2D.3
