题目内容
2.设点P、Q分别在直线3x-y+5=0和3x-y-13=0上运动,线段PQ中点为M(x0,y0),且x0+y0>4,则$\frac{y_0}{x_0}$的取值范围为[1,3).分析 设P(x1,y1),Q(x2,y2),则3x1-y1-5=0,3x2-y2-13=0,两式相加得3(x1+x2)-(y1+y2)-8=0,设M(x0,y0),则由中点的坐标公式可得3x0-y0-4=0,又x0+y0>4即点M在直线x+y=4上或者其右上方区域,画图得到M位于以(2,2)为端点向上的射线上,数形结合可得答案.
解答 解:设P,Q两点的坐标为P(x1,y1),Q(x2,y2),
∵点P,Q分别在直线3x-y+5=0和3x-y-13=0上运动,
∴3x1-y1-5=0,①
3x2-y2-13=0,②
两式相加得3(x1+x2)-(y1+y2)-8=0.
设线段PQ的中点M(x0,y0),
则x1+x2=2x0,y1+y2=2y0.
∴3x0-y0-4=0.
即y0=3x0-4.
又M点的坐标满足x0+y0>4,即M恒在直线x+y=4上或者其右上方区域,
∴线段PQ的中点M满足,如图.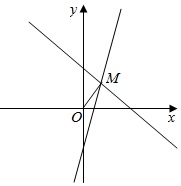
联立 $\left\{\begin{array}{l}{x+y=4}\\{y=3x-4}\end{array}\right.$,解得M(2,2),
∴M位于以(2,2)为端点向上的射线上,
当M(2,2)时,kOM=1,
∴直线OM斜率的取值范围是(1,3).
点评 本题考查了直线的斜率,考查了数学转化思想方法和数形结合的解题思想方法,属于中档题.

练习册系列答案
相关题目
17.已知集合S={x|x≤-1或x≥2},P={x|a≤x≤a+3},若S∪P=R,则实数a的取值集合为( )
| A. | {a|a≤0} | B. | {a|0≤a≤1} | C. | {a|a=1} | D. | {a|a=-1} |
11.已知正方形ABCD,则以A,B为焦点,且过C,D两点的椭圆的离心率为( )
| A. | $\sqrt{2}-1$ | B. | $\sqrt{3}-1$ | C. | $2-\sqrt{2}$ | D. | $3-\sqrt{5}$ |