题目内容
已知函数f(x)=-x2+4x+a,x∈[0,1],若f(x)有最小值-2,则f(x)的最大值为( )
A.-1 B.0
C.1 D.2
C解析: f(x)=-(x2-4x+4)+a+4=-(x-2)2+4+a.
∴函数f(x)图象的对称轴为x=2,
∴f(x)在[0,1]上单调递增.
又∵f(x)min=-2,∴f(0)=-2,即a=-2.
∴f(x)max=f(1)=-1+4-2=1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的解所在的区间( )
的解所在的区间( ) B.
B. C.
C. D.
D.
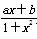 是定义在(-1,1)上的奇函数,且
是定义在(-1,1)上的奇函数,且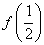 =
=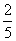 .
.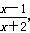 ,x∈[3,5].
,x∈[3,5]. 若f(a)<-3,则a的取值范围是________.
若f(a)<-3,则a的取值范围是________. 且过点(2,5)双曲线方程是( )
且过点(2,5)双曲线方程是( ) (B)
(B) (C)
(C) (D)
(D)