题目内容
设向量
,
,
满足|
|=|
|=1,
•
=-
,
-
,
-
的夹角为
,则|
|( )
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| c |
| b |
| c |
| π |
| 3 |
| c |
分析:
•
=|
||
|cos<
,
>=-
,求出<
,
>,利用向量减法的法则,判定向量
的终点在圆周上,这样可得答案.
| a |
| b |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| c |
解答:解:∵
•
=|
||
|cos<
,
>=-
,
∴cos<
,
>=-
.∴<
,
>=
,
∵
-
,
-
的夹角为
,如图:
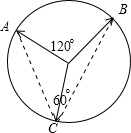
∴当C在优弧AB上时,|
|=|
|=1.
故选C.
| a |
| b |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
∴cos<
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| 2π |
| 3 |
∵
| a |
| c |
| b |
| c |
| π |
| 3 |

∴当C在优弧AB上时,|
| c |
| OC |
故选C.
点评:本题考查了向量的数量积公式,体现了数形结合思想.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目