题目内容
在△ABC中，tanAsin2B=tanBsin2A，那么△ABC一定是（ ）
| A、锐角三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等腰或直角三角形 |
考点：余弦定理
专题：解三角形
分析：已知等式利用同角三角函数间基本关系切化弦，以及二倍角的正弦函数公式化简，整理后再利用二倍角的余弦公式变形得到sin2A=sin2B，进而得到A=B，即可确定出三角形为等腰三角形．
解答：
解：在△ABC中，tanAsin2B=tanBsin2A，
化简得：
•2sinBcosB=
•2sinAcosA，
整理得：cos2B=cos2A，即
（1+cos2B）=
（1+cos2A），
化简得：cos2A=cos2B，
∴2A=2B，即A=B，
则△ABC为等腰三角形，
故选：C．
化简得：
| sinA |
| cosA |
| sinB |
| cosB |
整理得：cos2B=cos2A，即
| 1 |
| 2 |
| 1 |
| 2 |
化简得：cos2A=cos2B，
∴2A=2B，即A=B，
则△ABC为等腰三角形，
故选：C．
点评：此题考查了二倍角的正弦、余弦函数公式，以及同角三角函数间基本关系的运用，熟练掌握公式是解本题的关键．
练习册系列答案
应用题作业本系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知
=（2，1），
=（-1，k），如果
∥
，则实数k的值等于（ ）
| a |
| b |
| a |
| b |
| A、2 | ||
| B、-2 | ||
C、-
| ||
D、
|
已知不等式x2-ax+1＞0对任意x∈[0，2]恒成立，则实数a的取值范围为（ ）
A、（-∞，
| ||
| B、（-2，2） | ||
| C、[-2，2] | ||
| D、（-∞，2） |
正整数按下表的规律排列：则上起第2012行左起2013列的数为（ ）
| A、20122 |
| B、20132 |
| C、2011×2012 |
| D、2012×2013 |
设F1，F2是椭圆
+
=1的左、右两个焦点，若椭圆上满足PF1⊥PF2的点P有且只有两个，则离心率e的值为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
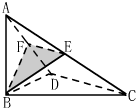如图，△BCD中，∠BCD=90°，AB⊥平面BCD，E，F分别为AC，AD的中点．