题目内容
已知函数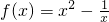 ,x∈(1,2],(Ⅰ)判断f(x)的单调性,并用定义证明你的结论;(Ⅱ)求f(x)的值域.
,x∈(1,2],(Ⅰ)判断f(x)的单调性,并用定义证明你的结论;(Ⅱ)求f(x)的值域.
解:(Ⅰ)解:f(x)在(1,2]上为增函数.证明如下:
设x1,x2是区间(1,2]上的任意两个实数且x1<x2,
则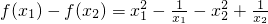
=(x1-x2)(x1+x2)- =(x1-x2)(x1+x2+
=(x1-x2)(x1+x2+ )
)
∵1<x1<x2≤2
∴x1+x2+ >0 x1-x2<0
>0 x1-x2<0
∴f(x1)-f(x2)<0 即f(x1)<f(x2)
∴f(x)在(1,2]上为增函数;
(Ⅱ)由(Ⅰ)f(x)在(1,2]上为增函数,
所以f(x)在(1,2]上的值域: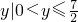 .
.
分析:(Ⅰ)任取3≤x1<x2≤5,我们构造出f(x2)-f(x1)的表达式,根据实数的性质,我们易出f(x2)-f(x1)的符号,进而根据函数单调性的定义,得到答案;
(Ⅱ)根据(1)可知函数的单调性,将区间端点的值代入即可求出函数的值域.
点评:本题主要考查函数单调性的判断与证明,以及应用单调性求函数的最值,同时还考查了学生的变形,转化能力,属中档题.
设x1,x2是区间(1,2]上的任意两个实数且x1<x2,
则
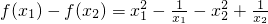
=(x1-x2)(x1+x2)-
 =(x1-x2)(x1+x2+
=(x1-x2)(x1+x2+ )
)∵1<x1<x2≤2
∴x1+x2+
 >0 x1-x2<0
>0 x1-x2<0∴f(x1)-f(x2)<0 即f(x1)<f(x2)
∴f(x)在(1,2]上为增函数;
(Ⅱ)由(Ⅰ)f(x)在(1,2]上为增函数,
所以f(x)在(1,2]上的值域:
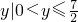 .
.分析:(Ⅰ)任取3≤x1<x2≤5,我们构造出f(x2)-f(x1)的表达式,根据实数的性质,我们易出f(x2)-f(x1)的符号,进而根据函数单调性的定义,得到答案;
(Ⅱ)根据(1)可知函数的单调性,将区间端点的值代入即可求出函数的值域.
点评:本题主要考查函数单调性的判断与证明,以及应用单调性求函数的最值,同时还考查了学生的变形,转化能力,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=ax-1+b
,其中a∈{0,1},b∈{1,2},则f(x)>0在x∈[-1,0]上有解的概率为( )
| 1-x2 |
A、
| ||
B、
| ||
C、
| ||
D、
|