题目内容
若 =
= ,
, =(sinωx,sinωx),其中ω>0,记函数f(x)=2
=(sinωx,sinωx),其中ω>0,记函数f(x)=2 •
• ,f(x)图象中相邻两条对称轴间的距离为
,f(x)图象中相邻两条对称轴间的距离为 ,
,
(1)求ω的值;
(2)求f(x)的单调减区间和f(x)的最大值及取得最大值时x的取值集合.
解:∵ =
= ,
, =(sinωx,sinωx)
=(sinωx,sinωx)
∴ •
• =
= sinωxcosωx+sin2ωx=
sinωxcosωx+sin2ωx= sin2ωx+
sin2ωx+ (1-cos2ωx)
(1-cos2ωx)
故f(x)=2 •
• =
= =
= …(4分)
…(4分)
(1)∵f(x)图象中相邻两条对称轴间的距离为
∴可得 ,解之得ω=1.…(6分)
,解之得ω=1.…(6分)
(2)由(1)得f (x)=2sin(2x- )+1
)+1
由 ,可得
,可得
∴f(x)的单调减区间为 …(8分)
…(8分)
当2x- =
= (k∈Z),即x=
(k∈Z),即x=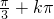 时,函数的最大值fmax(x)=3
时,函数的最大值fmax(x)=3
∴f(x)的最大值为3,取得最大值时x的取值集合为 …(12分)
…(12分)
分析:(1)根据向量数量积的坐标运算公式,结合二倍角的三角函数公式和辅助角公式化简得f(x)= ,再由正弦函数周期公式,建立ω的等式并解之即可得ω的值;
,再由正弦函数周期公式,建立ω的等式并解之即可得ω的值;
(2)根据正弦函数单调区间的公式解关于x的不等式,即可得到f(x)的单调减区间.再根据正弦函数的值域和函数取最大值时x的取值,解关于x的方程即可得到f(x)的最大值及取得最大值时x的取值集合.
点评:本题以向量的数量积运算为载体,给出三角函数式求函数的单调区间和周期,并求取得最大值时x的取值集合,着重考查了三角恒等变换和三角函数的图象与性质等知识,属于基础题.
 =
= ,
, =(sinωx,sinωx)
=(sinωx,sinωx)∴
 •
• =
= sinωxcosωx+sin2ωx=
sinωxcosωx+sin2ωx= sin2ωx+
sin2ωx+ (1-cos2ωx)
(1-cos2ωx)故f(x)=2
 •
• =
= =
= …(4分)
…(4分)(1)∵f(x)图象中相邻两条对称轴间的距离为

∴可得
 ,解之得ω=1.…(6分)
,解之得ω=1.…(6分)(2)由(1)得f (x)=2sin(2x-
 )+1
)+1由
 ,可得
,可得
∴f(x)的单调减区间为
 …(8分)
…(8分)当2x-
 =
= (k∈Z),即x=
(k∈Z),即x=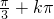 时,函数的最大值fmax(x)=3
时,函数的最大值fmax(x)=3∴f(x)的最大值为3,取得最大值时x的取值集合为
 …(12分)
…(12分)分析:(1)根据向量数量积的坐标运算公式,结合二倍角的三角函数公式和辅助角公式化简得f(x)=
 ,再由正弦函数周期公式,建立ω的等式并解之即可得ω的值;
,再由正弦函数周期公式,建立ω的等式并解之即可得ω的值;(2)根据正弦函数单调区间的公式解关于x的不等式,即可得到f(x)的单调减区间.再根据正弦函数的值域和函数取最大值时x的取值,解关于x的方程即可得到f(x)的最大值及取得最大值时x的取值集合.
点评:本题以向量的数量积运算为载体,给出三角函数式求函数的单调区间和周期,并求取得最大值时x的取值集合,着重考查了三角恒等变换和三角函数的图象与性质等知识,属于基础题.

练习册系列答案
相关题目
 ,n=(cos x,cos x),
,n=(cos x,cos x), .
.
 ,且边b所对的角θ的取值集合为M.当
,且边b所对的角θ的取值集合为M.当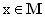 时,求函数f(x)=m·n的值域.
时,求函数f(x)=m·n的值域.