题目内容
如图, 是直三棱柱,
是直三棱柱, 为直角,点
为直角,点 、
、 分别是
分别是 、
、 的中点,若
的中点,若 ,则
,则 与
与 所成角的余弦值是( )
所成角的余弦值是( )
A. | B. | C. | D. |
D
解析试题分析:先取BC的中点D,连接D1F1,F1D,将BD1平移到F1D,则∠DF1A就是异面直线BD1与AF1所成角,在△DF1A中利用余弦定理求出此角即可.
解:取BC的中点D,连接D1F1,F1D,∴D1B∥D1F,∴∠DF1A就是BD1与AF1所成角设BC=CA=CC1=2,则AD= ,AF1=
,AF1= ,DF1=
,DF1= ,在△DF1A中,cos∠DF1A=
,在△DF1A中,cos∠DF1A= ,故选D
,故选D
考点:异面直线所成的角
点评:本小题主要考查异面直线所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
已知命题 ,
, 为直线,
为直线, 为平面,若
为平面,若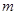 ∥
∥ ,
, ,则
,则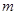 ∥
∥ ;命题
;命题 若
若 ,则
,则 ,则下列命题为真命题的是( )
,则下列命题为真命题的是( )
A. 或 或 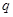 | B. 或 或 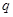 | C. 且 且 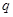 | D. 且 且 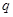 |
已知: ,
, ,
, ,则
,则 与
与 的位置关系是( )
的位置关系是( )
A. | B. |
C. , , 相交但不垂直 相交但不垂直 | D. , , 异面 异面 |
已知 、
、 、
、 是三条不同的直线,
是三条不同的直线, 、
、 、
、 是三个不同的平面,给出以下命题:
是三个不同的平面,给出以下命题:
①若 ,则
,则 ; ②若
; ②若 ,则
,则 ;③若
;③若 ,
, ,则
,则 ;④若
;④若 ,
, ,则
,则 .
.
其中正确命题的序号是( )
| A.②④ | B.②③ | C.③④ | D.①③ |
已知 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,则下列命题中正确的是( )
是三个不同的平面,则下列命题中正确的是( )
A. ,则 ,则 | B. ,则 ,则 |
C. ,则 ,则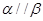 | D. ,则 ,则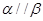 |
如图所示,在棱长为2的正方体 内(含正方体表面)任取一点
内(含正方体表面)任取一点 ,则
,则 的概率
的概率 ( )
( ) 
A. | B. | C. | D. |
已知 、
、 是不同的平面,
是不同的平面, 、
、 是不同的直线,则下列命题不正确的( )
是不同的直线,则下列命题不正确的( )
A.若 ∥ ∥ 则 则 | B.若 ∥ ∥ 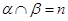 ,则 ,则 ∥ ∥ |
C.若 ∥ ∥ , , ,则 ,则 | D.若  则 则 ∥ ∥ |
 ,则这个二面角的大小为( )
,则这个二面角的大小为( )




 △ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=
△ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=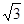 ,则点P 到△ABC的斜边AB的距离是( )
,则点P 到△ABC的斜边AB的距离是( ) 

