题目内容
18.${∫}_{-1}^{1}$(sinx+x2)dx=( )| A. | 0 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
分析 根据积分公式进行求解即可.
解答 解:${∫}_{-1}^{1}$(sinx+x2)dx=(-cosx+$\frac{1}{3}$x3)|${\;}_{-1}^{1}$=-cos1+$\frac{1}{3}$-[-cos(-1)-$\frac{1}{3}$]=$\frac{2}{3}$,
故选:C.
点评 本题主要考查积分的计算,要求熟练掌握掌握常见函数的积分,比较基础.

练习册系列答案
相关题目
6.把函数y=cos(2x+φ)(|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{6}$个单位,得到函数y=f(x)的图象关于直线x=$\frac{5π}{12}$对称,则φ的值为( )
| A. | -$\frac{π}{12}$ | B. | -$\frac{π}{6}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
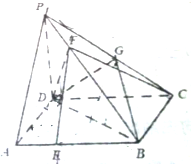 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC的中点,E,F分别为AB,PB上一点,AB=4$\sqrt{2}$,AE=$\sqrt{2}$,PB=4PF.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC的中点,E,F分别为AB,PB上一点,AB=4$\sqrt{2}$,AE=$\sqrt{2}$,PB=4PF.