题目内容
3．数列{an}的前n项和${S_n}=A{n^2}+Bn+q（A≠0）$，则q=0是{an}为等差数列的（ ）条件．| A． | 充分不必要 | B． | 必要不充分 | ||
| C． | 充要 | D． | 既不充分也不必要 |
分析 由等差数列的求和公式可得：Sn=na1+$\frac{n（n-1）}{2}$d=$\frac{d}{2}$n2+$（{a}_{1}-\frac{d}{2}）$n，即可判断出结论．
解答 解：由等差数列的求和公式可得：Sn=na1+$\frac{n（n-1）}{2}$d=$\frac{d}{2}$n2+$（{a}_{1}-\frac{d}{2}）$n，
因此q=0是{an}为等差数列的充要条件．
故选：C．
点评 本题考查了等差数列的求和公式、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
13．已知函数f（x）=|kx-1|．
（Ⅰ）若f（x）≤3的解集为[-2，1]，求实数k的值；
（Ⅱ）当k=1时，若对任意x∈R，不等式f（x+2）-f（2x+1）≤3-2m都成立，求实数m的取值范围．
（Ⅰ）若f（x）≤3的解集为[-2，1]，求实数k的值；
（Ⅱ）当k=1时，若对任意x∈R，不等式f（x+2）-f（2x+1）≤3-2m都成立，求实数m的取值范围．
14．在区间（0，4）上任取一实数x，则2x＜2的概率是（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
11．在正三棱柱ABC-A1B1C1中，已知AB=1，AA1=2，D为BB1的中点，则AD与平面AA1C1C所成角的余弦值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{\sqrt{6}}}{4}$ | D． | $\frac{{\sqrt{10}}}{4}$ |
8．已知F1，F2分别为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0，a≠b）$的左右焦点，P为双曲线右支上异于顶点的任一点，O为坐标原点，则下列说法正确的是（ ）
| A． | △PF1F2的内切圆圆心在直线$x=\frac{a}{2}$上 | B． | △PF1F2的内切圆圆心在直线x=b上 | ||
| C． | △PF1F2的内切圆圆心在直线OP上 | D． | △PF1F2的内切圆经过点（a，0） |
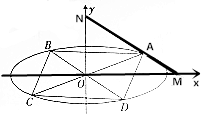已知椭圆O：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点（$\sqrt{3}$，-$\frac{1}{2}$），A（x0，y0）（x0y0≠0），其上顶点到直线$\sqrt{3}$x+y+3=0的距离为2，过点A的直线l与x，y轴的交点分别为M、N，且$\overrightarrow{AN}$=2$\overrightarrow{MA}$．
19．在△ABC中，若sin B•sin C=cos2$\frac{A}{2}$，且sin2B+sin2C=sin2A，则△ABC是（ ）
| A． | 等边三角形 | B． | 直角三角形 | C． | 等腰三角形 | D． | 等腰直角三角形 |