题目内容
10.在等比数列{an}中,${a_2}=4{,^{\;}}{a_5}=32$.(1)求数列{an}的通项公式;
(2)若${a_3}{,^{\;}}{a_5}$分别为等差数列{bn}的第4项和第16项,求数列{bn}的前n项和Sn.
分析 (1)设等比数列{an}的公比为q,由${a_2}=4{,^{\;}}{a_5}=32$.可得$\left\{\begin{array}{l}{{a}_{1}q=4}\\{{a}_{1}{q}^{4}=32}\end{array}\right.$,解出即可得出.
(2)b4=a3=8,b16=a5=32,可得$\left\{\begin{array}{l}{{b}_{1}+3d=8}\\{{b}_{1}+15d=32}\end{array}\right.$,解得b1,d.利用求和公式即可得出.
解答 解:(1)设等比数列{an}的公比为q,∵${a_2}=4{,^{\;}}{a_5}=32$.∴$\left\{\begin{array}{l}{{a}_{1}q=4}\\{{a}_{1}{q}^{4}=32}\end{array}\right.$,解得a1=q=2.∴an=2n.
(2)b4=a3=8,b16=a5=32,∴$\left\{\begin{array}{l}{{b}_{1}+3d=8}\\{{b}_{1}+15d=32}\end{array}\right.$,解得b1=d=2.
∴Sn=2n+$\frac{n(n-1)}{2}×2$=n2+n.
点评 本题考查了等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.在区间(0,4)上任取一实数x,则2x<2的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
15.“点M在曲线$\frac{x^2}{4}+\frac{y^2}{2}=1$上”是“点M的坐标满足方程$y=-\frac{{\sqrt{2}}}{2}\sqrt{4-{x^2}}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.已知i是虚数单位,若z(1+i)=1+3i,则z=( )
| A. | 2+i | B. | 2-i | C. | -1+i | D. | -1-i |
19.在△ABC中,若sin B•sin C=cos2$\frac{A}{2}$,且sin2B+sin2C=sin2A,则△ABC是( )
| A. | 等边三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等腰直角三角形 |
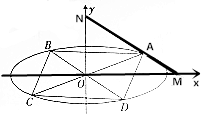 已知椭圆O:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点($\sqrt{3}$,-$\frac{1}{2}$),A(x0,y0)(x0y0≠0),其上顶点到直线$\sqrt{3}$x+y+3=0的距离为2,过点A的直线l与x,y轴的交点分别为M、N,且$\overrightarrow{AN}$=2$\overrightarrow{MA}$.
已知椭圆O:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点($\sqrt{3}$,-$\frac{1}{2}$),A(x0,y0)(x0y0≠0),其上顶点到直线$\sqrt{3}$x+y+3=0的距离为2,过点A的直线l与x,y轴的交点分别为M、N,且$\overrightarrow{AN}$=2$\overrightarrow{MA}$.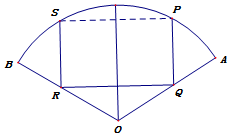 如图,扇形OAB的半径为1,圆心角为120°,四边形PQRS是扇形的内接矩形,当其面积最大时,求点P的位置,并求此最大面积.
如图,扇形OAB的半径为1,圆心角为120°,四边形PQRS是扇形的内接矩形,当其面积最大时,求点P的位置,并求此最大面积.