题目内容
5.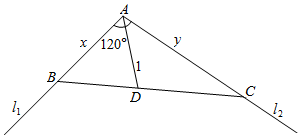 如图,某水域的两直线型岸边l1,l2 成定角120°,在该水域中位于该角角平分线上且与顶点A相距1公里的D处有一固定桩.现某渔民准备经过该固定桩安装一直线型隔离网BC(B,C分别在l1和l2上),围出三角形ABC养殖区,且AB和AC都不超过5公里.设AB=x公里,AC=y公里.
如图,某水域的两直线型岸边l1,l2 成定角120°,在该水域中位于该角角平分线上且与顶点A相距1公里的D处有一固定桩.现某渔民准备经过该固定桩安装一直线型隔离网BC(B,C分别在l1和l2上),围出三角形ABC养殖区,且AB和AC都不超过5公里.设AB=x公里,AC=y公里.(1)将y表示成x的函数,并求其定义域;
(2)该渔民至少可以围出多少平方公里的养殖区?
分析 (1)由S△ABD+S△ACD=S△ABC,将y表示成x的函数,由0<y≤5,0<x≤5,求其定义域;
(2)S=$\frac{1}{2}$xysinA=$\frac{1}{2}•x•\frac{x}{x-1}•$sin120°=$\frac{\sqrt{3}{x}^{2}}{4(x-1)}$($\frac{5}{4}$≤x≤5),变形,利用基本不等式,即可得出结论.
解答 解:(1)由S△ABD+S△ACD=S△ABC,得$\frac{1}{2}xsin60°+\frac{1}{2}ysin60°=\frac{1}{2}xysin120°$,
所以x+y=xy,所以y=$\frac{x}{x-1}$
又0<y≤5,0<x≤5,所以$\frac{5}{4}$≤x≤5,
所以定义域为{x|$\frac{5}{4}$≤x≤5};
(2)设△ABC的面积为S,则结合(1)得:S=$\frac{1}{2}$xysinA=$\frac{1}{2}•x•\frac{x}{x-1}•$sin120°=$\frac{\sqrt{3}{x}^{2}}{4(x-1)}$($\frac{5}{4}$≤x≤5)
$\frac{{x}^{2}}{x-1}$=(x-1)+$\frac{1}{x-1}$+2≥4,当仅当x-1=$\frac{1}{x-1}$,x=2时取等号.
故当x=y=2时,面积S取最小值\$\sqrt{3}$平方公里.
答:该渔民总共至少可以围出$\sqrt{3}$平方公里的养殖区.
点评 本题考查的是利用基本不等式解决实际问题,考查三角形面积的计算,正确计算面积,利用基本不等式是关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
15.已知公差不为零的等差数列{an}(n≥3)的最大项为正数.若将数列{an}中的项重新排列得到公比为q的等比数列{bn}.则下列说法正确的是( )
| A. | q>0时,数列{bn}中的项都是正数 | B. | 数列{an}中一定存在的为负数的项 | ||
| C. | 数列{an}中至少有三项是正数 | D. | 以上说法都不对 |
13.设当x=θ时,函数f(x)=2cosx-3sinx取得最小值,则tanθ等于( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
14.用红、黄、蓝、绿4种颜色为一个五棱锥的六个顶点着色,要求每一条棱的两个端点着不同的颜色,则不同的着色方案共有 ( )种?
| A. | 120 | B. | 140 | C. | 180 | D. | 240 |