题目内容

15．已知公差不为零的等差数列{an}（n≥3）的最大项为正数．若将数列{an}中的项重新排列得到公比为q的等比数列{bn}．则下列说法正确的是（　　）
A．q＞0时，数列{bn}中的项都是正数B．数列{an}中一定存在的为负数的项
C．数列{an}中至少有三项是正数D．以上说法都不对

分析 不妨设等差数列{an}中的每一项如下：a1＜a2＜a3＜…＜an，其中an＞0．如果数列{an}中至少有三项式正数，比如0＜an-2＜an-1＜an，这时，an-2，an-1，an即是等差数列又是等比数列，可得：an-2=an-1=an，矛盾．即可得出．

解答 解：不妨设等差数列{an}中的每一项如下：a1＜a2＜a3＜…＜an，其中an＞0．
如果数列{an}中至少有三项式正数，比如0＜an-2＜an-1＜an，这时，an-2，an-1，an即是等差数列又是等比数列，即an-2=an-1=an，矛盾．
说明数列{an}中至多有两项是正数．
∴数列{an}中一定存在的为负数的项．
故选：B．

点评 本题考查了等差数列与等比数列的通项公式及其性质、反证法，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
5．已知数列{an}为等差数列，a2=3，a4=7；数列{bn}为公比为q（q＞1）的等比数列，且满足集合{b1，b2，b3}={1，2，4}．
（Ⅰ）求数列{an}，{bn}的通项公式；
（Ⅱ）求数列{an+bn}的前n项和Sn．
6．不等式x2-4|x|-5＜0的解集是{x|-$\sqrt{5}$＜x＜$\sqrt{5}$}．．
3．已知函数$f（x）=\left\{\begin{array}{l}\frac{a}{x-1}，\;x≤0\\{log_2}x，\;x＞0.\end{array}\right.$
①若a=1，且关于x的方程f（x）=k有两个不同的实根，则实数k的取值范围是[-1，0）；
②若关于x的方程f（f（x））=0有且只有一个实根，则实数a的取值范围是（-1，0）∪（0，+∞）．
10．已知数列{an}的奇数项是首项为1的等差数列，偶数项是首项为2的等比数列．设数列{an}的前n项和为Sn，且满足a4=S3，a9=a3+a4．
（1）求数列{an}的通项公式；
（2）若akak+1=ak+2，求正整数k的值；
（3）是否存在正整数k，使得$\frac{{{S_{2k}}}}{{{S_{2k-1}}}}$恰好为数列{an}的一项？若存在，求出所有满足条件的正整数k；若不存在，请说明理由．
20．已知函数f（x）=2sin（ωx），其中常数ω＞0．
（1）若y=f（x）在$[-\frac{3π}{4}，\frac{π}{3}]$上单调递增，求ω的取值范围；
（2）令ω=2，将函数y=f（x）的图象向左平移$\frac{π}{6}$个单位长度，再向上平移1个单位长度，得到函数y=g（x）的图象，区间[a，b]（a＜b，a，b∈R）满足：y=g（x）在[a，b]上至少含有20个零点，在所有满足上述条件的[a，b]中，求b-a的最小值．
7．已知函数f（x）=aex-1-x2+bln（x+1）．
（1）当a=0，b=1时，求函数f（x）的单调区间；
（2）设函数f（x）在点（0，f（0））处的切线方程为x-ey+1=0，当x（-1，1]时，求证：f（x）＜$\frac{\sqrt{2}}{2}$．
4．若变量x，y满足约束条件$\left\{\begin{array}{l}{x-y≥-1}\\{x+y≤4}\\{y≥2}\\{\;}\end{array}\right.$，则目标函数z=2x+4y的最大值为（　　）
A．10B．11C．12D．13
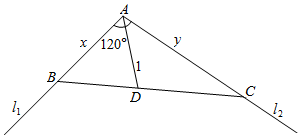5．如图，某水域的两直线型岸边l1，l2 成定角120°，在该水域中位于该角角平分线上且与顶点A相距1公里的D处有一固定桩．现某渔民准备经过该固定桩安装一直线型隔离网BC（B，C分别在l1和l2上），围出三角形ABC养殖区，且AB和AC都不超过5公里．设AB=x公里，AC=y公里．
（1）将y表示成x的函数，并求其定义域；
（2）该渔民至少可以围出多少平方公里的养殖区？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网