题目内容
4．已知某几何体的三视图如上图所示，则该几何体的体积为（ ）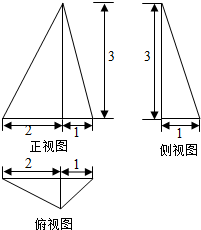
| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | 3 | D． | 1 |
分析 根据几何体的三视图，得出该几何体是三棱锥，结合图中数据求出它的体积．
解答 解：根据几何体的三视图，得；
该几何体是三棱锥，且底面三角形的边长为3，它边上的高为1，
三棱锥的高为3；
所以该三棱锥的体积为
V=$\frac{1}{3}$×$\frac{1}{2}$×3×1×3=$\frac{3}{2}$．
故选：C．
点评 本题考查了根据几何体的三视图求几何体的体积的应用问题，是基础题目．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
15．
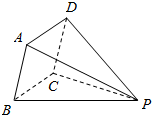各棱长都为2的四棱锥，底面ABCD是正方形，将侧面PBC水平放置，则这个几何体的俯视图的面积为（ ）
各棱长都为2的四棱锥，底面ABCD是正方形，将侧面PBC水平放置，则这个几何体的俯视图的面积为（ ）| A． | $\sqrt{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{4\sqrt{3}}{3}$ | D． | $\frac{5\sqrt{3}}{3}$ |
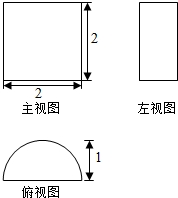
12．如图，下列四个几何体中，它们各自的三视图（主视图、左视图、俯视图）有两个相同，而另一个不同的几何体是（ ）
| A． | ①② | B． | ②③ | C． | ②④ | D． | ③④ |
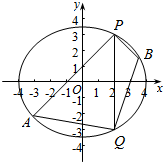已知椭圆C的中心在原点，一个焦点和抛物线y2=8x的焦点重合，离心率等于$\frac{1}{2}$．