题目内容
18.若函数f(x)=$\frac{a-sinx}{cosx}$在区间($\frac{π}{6}$,$\frac{π}{3}$)上单调递增,则实数a的取值范围是[2,+∞).分析 求函数的导数,根据函数单调性和导数之间的关系,建立不等式,利用参数分离法进行求解即可,
解答 解:函数f′(x)=$\frac{-co{s}^{2}x-(a-sinx)(-sinx)}{co{s}^{2}x}$=$\frac{-co{s}^{2}x+asinx-si{n}^{2}x}{co{s}^{2}x}$=$\frac{asinx-1}{co{s}^{2}x}$,
若f(x)在区间($\frac{π}{6}$,$\frac{π}{3}$)上单调递增,
则f′(x)≥0恒成立,即asinx-1≥0在区间($\frac{π}{6}$,$\frac{π}{3}$)上恒成立,
即asinx≥1,
则a≥$\frac{1}{sinx}$
∵$\frac{π}{6}$<x<$\frac{π}{3}$,∴$\frac{1}{2}$<sinx<$\frac{\sqrt{3}}{2}$,
∴$\frac{2\sqrt{3}}{3}$<$\frac{1}{sinx}$<2,
则a≥2
故答案为:[2,+∞)
点评 本题主要考查函数单调性和导数之间的关系,以及不等式恒成立问题,利用参数分离法是解决本题的关键,考查学生的运算和转化能力.

练习册系列答案
相关题目
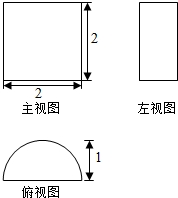
15.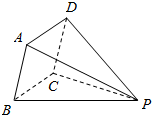 各棱长都为2的四棱锥,底面ABCD是正方形,将侧面PBC水平放置,则这个几何体的俯视图的面积为( )
各棱长都为2的四棱锥,底面ABCD是正方形,将侧面PBC水平放置,则这个几何体的俯视图的面积为( )
 各棱长都为2的四棱锥,底面ABCD是正方形,将侧面PBC水平放置,则这个几何体的俯视图的面积为( )
各棱长都为2的四棱锥,底面ABCD是正方形,将侧面PBC水平放置,则这个几何体的俯视图的面积为( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{5\sqrt{3}}{3}$ |