题目内容
如图2-1所示,在Rt△ABC中,已知BC=a,若长为2a的线段PQ以点A为中点,问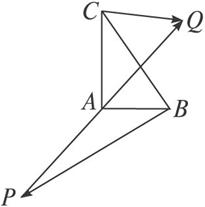
图2-1
解法一:如图,∵![]() ⊥
⊥![]() ,∴
,∴![]() ·
·![]() =0.
=0.

∵![]() =-
=-![]() ,
,![]() =
=![]() -
-![]() ,
,![]() =
=![]() -
-![]() ,
,
∴![]() ·
·![]() =(
=(![]() -
-![]() )·(
)·(![]() -
-![]() )
)
=![]() ·
·![]() -
-![]() ·
·![]() -
-![]() ·
·![]() +
+![]() ·
·![]()
=-a2-![]() ·
·![]() +
+![]() ·
·![]()
=-a2+![]() ·(
·(![]() -
-![]() )
)
=-a2+![]()
![]() ·
·![]()
=-a2+a2cosθ.
故当cosθ=1即θ=0(![]() 与
与![]() 方向相同)时,
方向相同)时, ![]() ·
·![]() 最大,其最大值为0.
最大,其最大值为0.
解法二:以直角顶点A为坐标原点,两直角边所在直线为坐标轴建立如图所示平面直角坐标系.
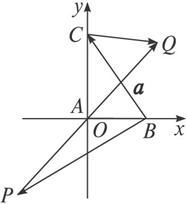
设|AB|=c,|AC|=b,则A(0,0),B(c,0),C(0,b),且|PQ|=2a,|BC|=a.
设点P的坐标为(x,y),则点Q(-x,-y).
∴![]() =(x-c,y),
=(x-c,y), ![]() =(-x,-y-b),
=(-x,-y-b),![]() =(-c,b),
=(-c,b),![]() =(-2x,-2y).
=(-2x,-2y).
∴![]() ·
·![]() =(x-c)(-x)+y(-y-b)=-(x2+y2)+cx-by.
=(x-c)(-x)+y(-y-b)=-(x2+y2)+cx-by.
∵cosθ=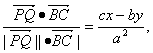
∴cx-by=a2cosθ.
∴![]() ·
·![]() =-a2+a2cosθ.
=-a2+a2cosθ.
故当cosθ=1,即θ=0(![]() 与
与![]() 方向相同)时,
方向相同)时, ![]() ·
·![]() 最大,其最大值为0.
最大,其最大值为0.

练习册系列答案
相关题目
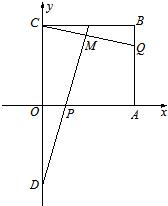 如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,
如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,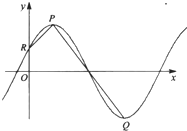 (2013•汕头一模)已知函数.f(x)=Asin(
(2013•汕头一模)已知函数.f(x)=Asin(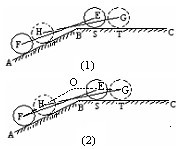 (2013•徐汇区一模)某种型号汽车四个轮胎半径相同,均为R=40cm,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为l=280cm (假定四个轮胎中心构成一个矩形).当该型号汽车开上一段上坡路ABC(如图(1)所示,其中∠ABC=a(
(2013•徐汇区一模)某种型号汽车四个轮胎半径相同,均为R=40cm,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为l=280cm (假定四个轮胎中心构成一个矩形).当该型号汽车开上一段上坡路ABC(如图(1)所示,其中∠ABC=a( (2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.
(2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.