Question

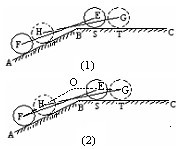（2013•徐汇区一模）某种型号汽车四个轮胎半径相同，均为R=40cm，同侧前后两轮胎之间的距离（指轮胎中心之间距离）为l=280cm （假定四个轮胎中心构成一个矩形）．当该型号汽车开上一段上坡路ABC（如图（1）所示，其中∠ABC=a（

3

4

π＜a＜π），且前轮E已在BC段上时，后轮中心在F位置；若前轮中心到达G处时，后轮中心在H处（假定该汽车能顺利驶上该上坡路）．设前轮中心在E和G处时与地面的接触点分别为S和T，且BS=60cm，ST=100cm．（其它因素忽略不计）
（1）如图（2）所示，FH和GE的延长线交于点O，求证：OE=40cot

α

2

+60（cm）；
（2）当a=

5

6

π时，后轮中心从F处移动到H处实际移动了多少厘米？（精确到1cm）

Answer 1

分析：（1）依题意，∠EOH=α，由Rt△OMB

∽

.

Rt△ONB，可求得∠BOM=

α

2

，在Rt△OMB中，可求得OM=40cot

α

2

，从而可证得结论；
（2）由（1）结论得OE=

40

tan75°

+60，设OH=x，OF=y，在△OHG中，由余弦定理可求得x，在△OEF中，由余弦定理可求得y，而FH=y-x，从而可得答案．

解答：解：（1）由OE∥BC，OH∥AB，得∠EOH=α，…..（2分）
过点B作BM⊥OE，BN⊥OH，则
Rt△OMB

∽

.

Rt△ONB，从而∠BOM=

α

2

．…..（4分）
在Rt△OMB中，由BM=40得OM=40cot

α

2

，从而，OE=OM+ME=OM+BS=40cot

α

2

+60．…..（6分）
（2）由（1）结论得OE=

40

tan75°

+60．
设OH=x，OF=y，在△OHG中，由余弦定理得，
280²=x²+（

40

tan75°

+60+100）²-2x（

40

tan75°

+60+100）cos150°，
解得x≈118.8cm．…..（9分）
在△OEF中，由余弦定理得，
280²=y²+（

40

tan75°

+60）²-2y（

40

tan75°

+60）cos150°，
解得y≈216.5cm．…..（12分）
所以，FH=y-x≈98cm，
即后轮中心从F处移动到H处实际移动了约98cm．…（14分）

点评：本题考查余弦定理，考查根据实际问题选择函数类型，着重考查分析理解与运算能力，属于中档题．