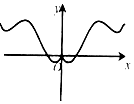
题目内容
5.有以下判断:①$f(x)=\frac{|x|}{x}$与g(x)=$\left\{\begin{array}{l}{1,x≥0}\\{-1,x<0}\end{array}\right.$表示同一函数;
②“x=2”是“x2>4”的必要而不充分条件;
③若f(x)=|x|-|x-1|,则$f[f(\frac{1}{2})]$=0;
④若x2-2x=0,则x=2的逆命题是真命题
其中正确的序号为④.
分析 由函数定义域不同判断①;求出不等式x2>4的解集,结合充分必要条件的判定方法判断②;直接求出函数值判断③;写出命题的逆命题判断④.
解答 解:①$f(x)=\frac{|x|}{x}$的定义域为{x|x≠0},g(x)=$\left\{\begin{array}{l}{1,x≥0}\\{-1,x<0}\end{array}\right.$的定义域为R,定义域不同,不是同一函数,故①错误;
②由x2>4,得x<-2或x>2,∴“x=2”是“x2>4”的既不充分也不必要条件,故②错误;
③若f(x)=|x|-|x-1|,则f($\frac{1}{2}$)=|$\frac{1}{2}$|-|$\frac{1}{2}-1$|=$\frac{1}{2}-\frac{1}{2}=0$,∴$f[f(\frac{1}{2})]$=f(0)=-1,故③错误;
④若x2-2x=0,则x=2的逆命题是若x=2,则x2-2x=0,是真命题,故④正确.
∴正确命题的序号是④.
故答案为:④.
点评 本题考查命题的真假判断与应用,考查函数值的求法,考查了充分必要条件的判定方法,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.圆(x-1)2+(y+1)2=10的半径为( )
| A. | (1,-1) | B. | (-1,1) | C. | $\sqrt{10}$ | D. | 10 |
20.设x,y满足约束条件$\left\{{\begin{array}{l}{2x-y-2≤0}\\{x-2y+2≥0}\\{x+y-2≥0}\end{array}}\right.$若z=mx+y取得最大值时的最优解有无穷多个,则实数m的值是( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 1 |
14.某多面体的三视图如下图所示(网格纸上小正方形的边长为1),则该多面体的表面积为( )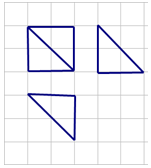

| A. | $8+4\sqrt{2}$ | B. | $6+4\sqrt{2}$ | C. | 12 | D. | $8+5\sqrt{2}$ |
15.已知向量$\overrightarrow a=(2cosθ,2sinθ),\overrightarrow b=(0,-2)$,$θ∈(\frac{π}{2},π)$,则向量夹角为( )
| A. | $\frac{3π}{2}-θ$ | B. | $θ-\frac{π}{2}$ | C. | $\frac{π}{2}+θ$ | D. | θ |