题目内容
函数f（x）=2x+lnx在x=1处的切线方程为 ．
【答案】分析：由f（x）=2x+lnx，知f（1）=2，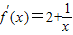
，k=f′（1）=3，由此能求出f（x）在x=1处的切线方程．
解答：解：∵f（x）=2x+lnx，
∴f（1）=2，
，
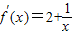∴k=f′（1）=3，
∴f（x）在x=1处的切线方程为y-2=3（x-1），即3x-y-1=0．
故答案为：3x-y-1=0．
点评：本题考查函数的切线方程的求法，是基础题．解题时要认真审题，仔细解答．
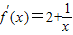，k=f′（1）=3，由此能求出f（x）在x=1处的切线方程．解答：解：∵f（x）=2x+lnx，
∴f（1）=2，
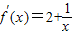，∴k=f′（1）=3，
∴f（x）在x=1处的切线方程为y-2=3（x-1），即3x-y-1=0．
故答案为：3x-y-1=0．
点评：本题考查函数的切线方程的求法，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
相关题目
设函数f（x）=
，则满足f（x）=4的x的值是（ ）
|
| A、2 | B、16 |
| C、2或16 | D、-2或16 |