题目内容
7. 某工厂要建造一个长方体形无盖贮水池,其容积为4800m3,深为3m,如果池底每平方米的造价为150元,池壁每平方米的造价为120元,设长方体底面长为xm,由于地形限制,0<x≤a,水池总造价为f(x)元.
某工厂要建造一个长方体形无盖贮水池,其容积为4800m3,深为3m,如果池底每平方米的造价为150元,池壁每平方米的造价为120元,设长方体底面长为xm,由于地形限制,0<x≤a,水池总造价为f(x)元.(1)求f(x)的解析式;
(2)求f(x)的最小值.
分析 (1)分别计算池底与池壁的造价,可得f(x)的解析式;
(2)分类讨论,利用基本不等式及函数的单调性,可求f(x)的最小值.
解答 解:(1)因水池底面一边的长度为xm,则另一边的长度为$\frac{4800}{3x}$m,--(1分)
根据题意,得f(x)=150×$\frac{4800}{3}$+120(2×3x+2×3×$\frac{4800}{3x}$)=240000+720(x+$\frac{1600}{x}$)
∴所求的函数表达式为:f(x)=720(x+$\frac{1600}{x}$)+240000(0<x≤a)-----------(6分)
(2)由(1)得,a≥40,f(x)=720(x+$\frac{1600}{x}$)+240000≥720×2$\sqrt{x•\frac{1600}{x}}$+240000-----------(9分)
=720×2×40+240000=297600.-----------(10分)
当且仅当x=$\frac{1600}{x}$,即x=40时,f(x)有最小值297600.
a<40时,y=x+$\frac{1600}{x}$在(0,a]上单调递减,∴x=a时,f(x)有最小值720(a+$\frac{1600}{a}$)+240000(---12分)
点评 本题考查函数模型的构建,考查利用基本不等式求最值,考查利用数学知识解决实际问题,属于中档题.

练习册系列答案
相关题目
15.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),若焦点F(c,0)关于渐近线y=$\frac{b}{a}$x的对称点在另一条渐近线y=-$\frac{b}{a}$x上,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
12.已知命题p:在调查某校高一学生的平均身高时宜采用系统抽样;命题q:在频率分布直方图中,中位数左边和右边的直方图的面积相等,则下列命题中为真命题的是( )
| A. | ¬q | B. | p∨(¬q) | C. | (¬p)∧q | D. | p∧q |
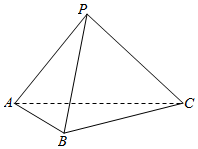 如图,点P是△ABC所在平面外的一点,PA=PB=PC=AB=BC=AC=1,F为AP的中点.
如图,点P是△ABC所在平面外的一点,PA=PB=PC=AB=BC=AC=1,F为AP的中点.