题目内容
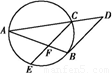
如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于点D.过点C作BD的平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,EF=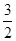
,则线段CD的长为 .
【答案】
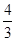
【解析】由相交弦定理知AF×FB=EF×FC,
又∵AF=3,FB=1,EF=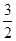
,
∴FC=2,
又∵FC∥BD,∴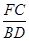
=
=
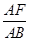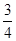,∴BD=
,
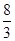又∵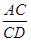
=
=
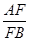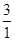,∴AD=4CD.
又由切割线定理知DB2=DC·DA,
∴
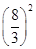=4CD2,∴CD=.
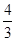练习册系列答案
寒假学与练系列答案
相关题目
（2012•天津）如图，已知AB和AC是圆的两条弦，过点B作圆的切线与AC的延长线相交于点D，过点C作BD的平行线与圆相交于点E，与AB相交于点F，AF=3，FB=1，EF=
（几何证明选讲选做题）
使
成立，则实数
的取值集合是__________．
，则线段CD的长为________．
：
（t为参数）与圆C2：
（
为参数）的位置关系不可能是________.
使
成立，则实数
的取值集合是__________．
，则线段CD的长为________．
：
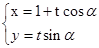（t为参数）与圆C2：
（
为参数）的位置关系不可能是________.
，则线段CD的长为____________.