题目内容
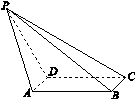
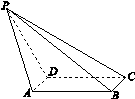
（2012•天津）如图，已知AB和AC是圆的两条弦，过点B作圆的切线与AC的延长线相交于点D，过点C作BD的平行线与圆相交于点E，与AB相交于点F，AF=3，FB=1，EF=| 3 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
分析：由相交弦定理求出FC，由相似比求出BD，设DC=x，则AD=4x，再由切割线定理，BD2=CD•AD求解．
解答：解：由相交弦定理得到AF•FB=EF•FC，即3×1=
×FC，FC=2，在△ABD中AF：AB=FC：BD，即3：4=2：BD，BD=
，
设DC=x，则AD=4x，再由切割线定理，BD2=CD•AD，即x•4x=（
）2，x=
故答案为：
| 3 |
| 2 |
| 8 |
| 3 |
设DC=x，则AD=4x，再由切割线定理，BD2=CD•AD，即x•4x=（
| 8 |
| 3 |
| 4 |
| 3 |
故答案为：
| 4 |
| 3 |
点评：本题主要考查了平面几何中直线与圆的位置关系，相交弦定理，切割线定理，相似三角形的概念、判定与性质．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
（2012•天津）如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AC=1．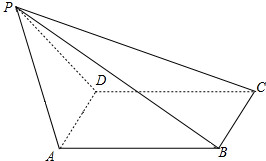
（2012•天津）如图，在四棱锥P-ABCD中，底面ABCD是矩形，AD⊥PD，BC=1，PC=2
，PD＝CD＝2.
，PD＝CD＝2.