题目内容

A．（不等式选做题）若不存在实数使成立，则实数的取值集合是__________．

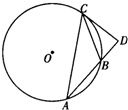
B． (几何证明选做题) )如图，已知AB和AC是圆的两条弦，过点B作圆的切线与AC的延长线相交于点D.过点C作BD的平行线与圆相交于点E，与AB相交于点F，AF＝3，FB＝1，EF＝，则线段CD的长为________．

C. (坐标系与参数方程选做题) 已知直线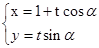：（t为参数）与圆C2：（为参数）的位置关系不可能是________.

 

【答案】

A.  B.     C. 相离.

【解析】

试题分析：因为A，不存在实数使成立，则 实数的取值集合是

对于B,由于解：由相交弦定理可得：3×1= ×FC，∴FC=2∵BD∥CF，∴CF:BC=AF:AB，∴BD=,设CD=x，则AD=4x，∵BD是圆的切线，,∴由切割线定理可得()2=x×4x,∴x=,故答案为

对于C,由于直线：（t为参数）与圆C2：，可以通过圆心（0，0）到直线的距离于圆的半径的大小1可知，距离小于或者等于半径1，故不可能是相离。

考点： 参数方程，几何证明，绝对值不等式

点评：解决的关键是对于绝对值不等式的最值，以及直线与圆的位置关系，和相交弦定理的熟练的运用，属于基础题。

 

练习册系列答案
相关题目
精英家教网A．（不等式选做题）
函数f（x）=x2-x-a2+a+1对于任一实数x，均有f（x）≥0．则实数a满足的条件是
 
．
B．（几何证明选做题）
如图，圆O是△ABC的外接圆，过点C的切线交AB的延长线于点D，CD=2
3
，AB=BC=4，则AC的长为
 
．
C．（坐标系与参数方程选做题）
在极坐标系中，曲线ρ=4cos(θ-
π
3
)上任意两点间的距离的最大值为
 
．
精英家教网A．（不等式选做题）不等式|3x-6|-|x-4|＞2x的解集为
 
．

B．（几何证明选做题）如图，直线PC与圆O相切于点C，割线PAB经过圆心O，
弦CD⊥AB于点E，PC=4，PB=8，则CE=
 
．
C．（坐标系与参数方程选做题）在极坐标系中，圆ρ=4cosθ的圆心到直线ρsin(θ+
π
4
)=2
2
的距离为
 
．
（请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
A．（不等式选做题）若不等式|x+1|+|x-2|≥a对任意x∈R恒成立，则a的取值范围是
 
．
B．（几何证明选做题）如图，∠B=∠D，AE⊥BC，∠ACD=90°，且AB=6，AC=4，AD=12，则AE=
 
．
精英家教网
C．（坐标系与参数方程选做题）直角坐标系xoy中，以原点为极点，x轴的正半轴为极轴建极坐标系，设点A，B分别在曲线C1：
x=3+cosθ
y=sinθ
 （θ为参数）和曲线C2：p=1上，则|AB|的最小值为
 
．
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
A．（不等式选做题）不等式|x-5|+|x+3|≥10的解集是
{x|x≥6或x≤-4}
{x|x≥6或x≤-4}
．
B．（坐标系与参数方程选做题）在极坐标系中，圆ρ=-2sinθ的圆心的极坐标是
（1，
3π
2
）
（1，
3π
2
）
．
C．（几何证明选做题）如图，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF=CF=2
2
，BE=1，BF=2，若CE与圆相切，则线段CE的长为
7
7
．
选做题：（考生注意：请在下列三题中任选一题作答，如果多做，则按所做第一题评分）
A．（不等式选做题）不等式
x+5
(x-1)2
≥2的解集是
[-
1
2
，1）∪（1，3]
[-
1
2
，1）∪（1，3]
．
B．（几何证明选做题） 如图，⊙O的直径AB=6cm，P是延长线上的一点，过点P作⊙O的切线，切点为C，连接AC，若∠CAP=30°，则PC=
3
3
3
3
．
C．（坐标系与参数方程选做题）已知直线x+2y-4=0与
x=2-3cosθ
y=1+3sinθ
（θ为参数）相交于A、B两点，则|AB|=
6
6
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网