题目内容
4.已知数列{an}的首项a1=1,且满足(an+1-1)an+an+1=0(n∈N*).(1)求数列{an}的通项公式;
(2)设cn=$\frac{3^n}{a_n}$,求数列{cn}的前n项和Sn.
分析 (1)由满足(an+1-1)an+an+1=0(n∈N*).整理得$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=1,利用等差数列的通项公式即可得出.
(2)由(1)知:cn=$\frac{3^n}{a_n}$=n•3n,再利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(1)由满足(an+1-1)an+an+1=0(n∈N*).
整理得$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=1,
∴数列$\{\frac{1}{{a}_{n}}\}$是等差数列,首项与公差都为1.
∴$\frac{1}{{a}_{n}}$=1+(n-1)=n,
∴an=$\frac{1}{n}$.
(2)由(1)知:cn=$\frac{3^n}{a_n}$=n•3n,
∴数列{cn}的前n项和Sn=3+2×32+3×33+…+n•3n,
∴3Sn=32+2×33+…+(n-1)•3n+n•3n+1,
∴-2Sn=3+32+…+3n-n•3n+1=$\frac{3({3}^{n}-1)}{3-1}$-n•3n+1=$\frac{1-2n}{2}$×3n+1-$\frac{3}{2}$,
∴Sn=$\frac{2n-1}{4}$×3n+1+$\frac{3}{4}$.
点评 本题考查了等差数列的通项公式及其前n项和公式、“错位相减法”,考查了变形推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知数列{an}为等差数列,数列{bn}满足bn=an+n,若b2,b5,b11成等比数列,且b3=a6.
(1)求an,bn;
(2)求数列{$\frac{1}{a_nb_n}$}的前n项和Sn.
(1)求an,bn;
(2)求数列{$\frac{1}{a_nb_n}$}的前n项和Sn.
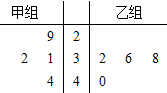 某商场为推销当地的某种特产进行了一次促销活动,将派出的促销员分成甲、乙两个小组分别在两个不同的场地进行促销,每个小组各4人.以下茎叶图记录了这两个小组成员促销这种特产的件数.
某商场为推销当地的某种特产进行了一次促销活动,将派出的促销员分成甲、乙两个小组分别在两个不同的场地进行促销,每个小组各4人.以下茎叶图记录了这两个小组成员促销这种特产的件数.