题目内容
13.函数f(x)=cos(ωx+$\frac{π}{6}$)(ω>0)在[0,π]内的值域为[-1,$\frac{\sqrt{3}}{2}$],则ω的取值范围是( )| A. | [$\frac{3}{2}$,$\frac{5}{3}$] | B. | [$\frac{5}{6}$,$\frac{3}{2}$] | C. | [$\frac{5}{6}$,+∞) | D. | [$\frac{5}{6}$,$\frac{5}{3}$] |
分析 根据余弦函数的图象与性质,结合题意得出π≤ωπ+$\frac{π}{6}$≤$\frac{11π}{6}$,
从而求出ω的取值范围.
解答 解:函数f(x)=cos(ωx+$\frac{π}{6}$)(ω>0),
当x∈[0,π]时,f(x)∈[-1,$\frac{\sqrt{3}}{2}$],
∴-1≤cos(ωx+$\frac{π}{6}$)≤$\frac{\sqrt{3}}{2}$,画出图形如图所示;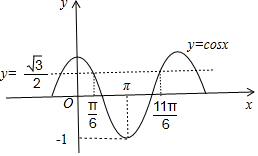
则π≤ωπ+$\frac{π}{6}$≤$\frac{11π}{6}$,
解得$\frac{5}{6}$≤ω≤$\frac{5}{3}$,
∴ω的取值范围是[$\frac{5}{6}$,$\frac{5}{3}$].
故选:D.
点评 本题考查了余弦函数的图象与性质的应用问题,是基础题.

练习册系列答案
相关题目
18. 执行如图所示的程序框图,若输入的x为4,则运行的次数与输出x的值分别为( )
执行如图所示的程序框图,若输入的x为4,则运行的次数与输出x的值分别为( )
 执行如图所示的程序框图,若输入的x为4,则运行的次数与输出x的值分别为( )
执行如图所示的程序框图,若输入的x为4,则运行的次数与输出x的值分别为( )| A. | 5.730 | B. | 5.729 | C. | 4.244 | D. | 4.243 |
5.某市春节期间7家超市广告费支出xi(万元)和销售额yi(万元)数据如表:
(Ⅰ)若用线性回归模型拟合y与x的关系,求y与x的线性回归方程.
(Ⅱ)若用二次函数回归模型拟合y与x的关系,可得回归方程:$\hat y=-0.17{x^2}$+5x+20,经计算二次函数回归模型和线性回归模型的R2分别约为0.93和0.75,请用R2说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出3万元时的销售额.
参考数据:$\overline x=8,\overline y=42,\sum_{i=1}^7{x_i}{y_i}=2794,\sum_{i=1}^7{{x_i}^2}$=708.
参考公式:$\hat b=\frac{{\sum_{i=1}^n{x_i}{y_i}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$$,\hat a=\overline y-\hat b\overline x$.
| 超市 | A | B | C | D | E | F | G |
| 广告费支出xi | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
| 销售额yi | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(Ⅱ)若用二次函数回归模型拟合y与x的关系,可得回归方程:$\hat y=-0.17{x^2}$+5x+20,经计算二次函数回归模型和线性回归模型的R2分别约为0.93和0.75,请用R2说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出3万元时的销售额.
参考数据:$\overline x=8,\overline y=42,\sum_{i=1}^7{x_i}{y_i}=2794,\sum_{i=1}^7{{x_i}^2}$=708.
参考公式:$\hat b=\frac{{\sum_{i=1}^n{x_i}{y_i}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$$,\hat a=\overline y-\hat b\overline x$.
1.执行如图所示程序框图,则输出的S的值为( )


| A. | 4 | B. | 8 | C. | -20 | D. | -4 |
 的单调增区间是_________.
的单调增区间是_________.
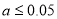 ”,请写出输出的所有数值;
”,请写出输出的所有数值;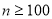 ”,试求出所有输出数字的和。
”,试求出所有输出数字的和。