题目内容
在等腰三角形ABC中,AB=AC,D在线段AC上,AD=kAC(k为常数,且0<k<1),BD=l为定长,则△ABC的面积最大值为 .
考点:正弦定理
专题:解三角形
分析:如图所示,以B为原点,BD为x轴建立平面直角坐标系,设A(x,y),y>0,根据题意得到AD=kAB,两边平方得到关系式,利用勾股定理化简后表示出y2,变形后利用二次函数的性质求出y的最大值,进而确定出三角形ABD面积的最大值,根据AD=kAC即可得出三角形ABC面积的最大值.
解答:
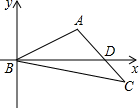 解:如图所示,以B为原点,BD为x轴建立平面直角坐标系,设A(x,y),y>0,
解:如图所示,以B为原点,BD为x轴建立平面直角坐标系,设A(x,y),y>0,
∵AB=AC,
∴AD=kAC=kAB,即AD2=k2AB2,
∴(x-l)2+y2=k2(x2+y2),
整理得:y2=
=
≤
,
∴ymax=
,
∵BD=l,
∴(S△ABD)max=
,
则(S△ABC)max=
(S△ABD)max=
.
故答案为:
 解:如图所示,以B为原点,BD为x轴建立平面直角坐标系,设A(x,y),y>0,
解:如图所示,以B为原点,BD为x轴建立平面直角坐标系,设A(x,y),y>0,∵AB=AC,
∴AD=kAC=kAB,即AD2=k2AB2,
∴(x-l)2+y2=k2(x2+y2),
整理得:y2=
| -(1-k2)x2+2lx-l2 |
| 1-k2 |
-(1-k2)(x-
| ||||
| 1-k2 |
| k2l2 |
| (1-k2)2 |
∴ymax=
| kl |
| 1-k2 |
∵BD=l,
∴(S△ABD)max=
| kl2 |
| 2(1-k2) |
则(S△ABC)max=
| 1 |
| k |
| l2 |
| 2(1-k2) |
故答案为:
| l2 |
| 2(1-k2) |
点评:此题考查了二次函数的性质,坐标与图形性质,弄清题意是解本题的关键.

练习册系列答案
相关题目
椭圆
+
=1(a>b>0)上两点A、B与中心O的连线互相垂直,则
+
的值为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| OA2 |
| 1 |
| OB2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知A、B、C三点共线,且满足m
-2
+
=
,则( )
| OA |
| OB |
| OC |
| 0 |
| A、A是BC的中点 |
| B、B是AC的中点 |
| C、C是AB的三等分点 |
| D、A是CB的三等分点 |