题目内容
2.已知P,Q分别是直线l:x-y-2=0和圆C:x2+y2=1上的动点,圆C与x轴正半轴交于点A(1,0),则|PA|+|PQ|的最小值为( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{5}-1$ | D. | $\frac{\sqrt{2}+\sqrt{10}}{2}$-1 |
分析 由题意画出图形,求出A关于直线l的对称点B的坐标,再求出B到圆心的距离,则答案可求.
解答 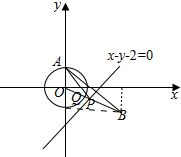 解:如图,圆C:x2+y2=1的圆心O(0,0),半径r=1,
解:如图,圆C:x2+y2=1的圆心O(0,0),半径r=1,
设A(1,0)关于l:x-y-2=0的对称点为B(a,b),
则$\left\{\begin{array}{l}{\frac{a+1}{2}-\frac{b}{2}-2=0}\\{\frac{b}{a-1}=-1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$,即B(2,-1),
连接BO,交直线l:x-y-2=0与P,
则|PA|+|PQ|的最小值为|BO|-r=$\sqrt{5}-1$.
故选:C.
点评 本题考查直线与圆的位置关系,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7. 执行如图所示的程序框图,则输出的n=( )
执行如图所示的程序框图,则输出的n=( )
 执行如图所示的程序框图,则输出的n=( )
执行如图所示的程序框图,则输出的n=( )| A. | 63 | B. | 66 | C. | -93 | D. | -69 |
11.二项式${(9x-\frac{1}{{3\root{3}{x}}})^9}$的展开式中x的系数等于( )
| A. | 84 | B. | 24 | C. | 6 | D. | -24 |
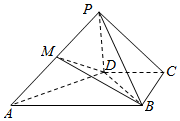 在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB=4,AB∥CD,∠BCD=90°,M为棱PA的中点.
在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB=4,AB∥CD,∠BCD=90°,M为棱PA的中点.
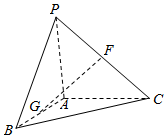 如图,在三棱锥P-ABC中,F、G、H分别是PC、AB、BC的中点,PA⊥平面ABC,PA=AB=AC=2,二面角B-PA-C为120°.
如图,在三棱锥P-ABC中,F、G、H分别是PC、AB、BC的中点,PA⊥平面ABC,PA=AB=AC=2,二面角B-PA-C为120°.