题目内容
已知函数
(Ⅰ)若a=-4,求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在[1,+∞)上单调递增,求实数a的取值范围
(Ⅲ)记函数g(x)=x2f'(x),若g(x)的最小值是-6,求函数f(x)的解析式.
解:(Ⅰ)由题意得, .由函数的定义域为x>0,
.由函数的定义域为x>0,
∴f'(x)>0?x> ,f'(x)<0?0<x<
,f'(x)<0?0<x< .
.
∴函数的单调递减区间为(0, ),单调递增区间为(
),单调递增区间为( ,+∞)
,+∞)
(Ⅱ)
函数f(x)在[1,+∞)上单调递增,∴f′(x)≥0在[1,+∞)上恒成立
∴ 在[1,+∞)上恒成立
在[1,+∞)上恒成立
令 ,x∈[1,+∞),则问题等价于a≥h(x)max
,x∈[1,+∞),则问题等价于a≥h(x)max
∵ 在[1,+∞)上单调递减
在[1,+∞)上单调递减
∴h(x)max=h(1)=0,∴a≥0
(Ⅲ)g(x)=x2f'(x)=2x3+ax-2,g′(x)=6x2+a
①a≥0,g,(x)=6x2+a>0恒成立,g(x)在(0,+∞)上单调递增,
∴g(x)没有最小值.
②a<0,g,(x)=6x2+a=0,∴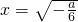
∴函数在(0,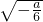 )上单调递减,在(
)上单调递减,在(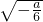 ,+∞)上单调递增
,+∞)上单调递增
∴g(x)在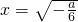 处取得最小值
处取得最小值
∴ ,∴a=-6
,∴a=-6
∴
分析:(Ⅰ)把a=-4代入得f(x),求出f′(x)>0得函数的增区间,求出f′(x)<0得到函数的减区间;
(Ⅱ) ,函数f(x)在[1,+∞)上单调递增,等价于f′(x)≥0在[1,+∞)上恒成立,利用分离参数法可得
,函数f(x)在[1,+∞)上单调递增,等价于f′(x)≥0在[1,+∞)上恒成立,利用分离参数法可得 在[1,+∞)上恒成立,求右边函数的最大值,即可求出实数a的取值范围;
在[1,+∞)上恒成立,求右边函数的最大值,即可求出实数a的取值范围;
(Ⅲ)g(x)=x2f'(x)=2x3+ax-2,g′(x)=6x2+a,分类讨论求出函数的最小值点.利用g(x)的最小值是-6,可求函数f(x)的解析式.
点评:本题以函数为载体,考查导数的运用,考查利用导数求函数的单调区间,考查函数的最值,考查学生等价转化问题的能力.
 .由函数的定义域为x>0,
.由函数的定义域为x>0,∴f'(x)>0?x>
 ,f'(x)<0?0<x<
,f'(x)<0?0<x< .
.∴函数的单调递减区间为(0,
 ),单调递增区间为(
),单调递增区间为( ,+∞)
,+∞)(Ⅱ)

函数f(x)在[1,+∞)上单调递增,∴f′(x)≥0在[1,+∞)上恒成立
∴
 在[1,+∞)上恒成立
在[1,+∞)上恒成立令
 ,x∈[1,+∞),则问题等价于a≥h(x)max
,x∈[1,+∞),则问题等价于a≥h(x)max∵
 在[1,+∞)上单调递减
在[1,+∞)上单调递减∴h(x)max=h(1)=0,∴a≥0
(Ⅲ)g(x)=x2f'(x)=2x3+ax-2,g′(x)=6x2+a
①a≥0,g,(x)=6x2+a>0恒成立,g(x)在(0,+∞)上单调递增,
∴g(x)没有最小值.
②a<0,g,(x)=6x2+a=0,∴
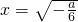
∴函数在(0,
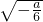 )上单调递减,在(
)上单调递减,在(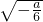 ,+∞)上单调递增
,+∞)上单调递增∴g(x)在
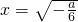 处取得最小值
处取得最小值∴
 ,∴a=-6
,∴a=-6∴

分析:(Ⅰ)把a=-4代入得f(x),求出f′(x)>0得函数的增区间,求出f′(x)<0得到函数的减区间;
(Ⅱ)
 ,函数f(x)在[1,+∞)上单调递增,等价于f′(x)≥0在[1,+∞)上恒成立,利用分离参数法可得
,函数f(x)在[1,+∞)上单调递增,等价于f′(x)≥0在[1,+∞)上恒成立,利用分离参数法可得 在[1,+∞)上恒成立,求右边函数的最大值,即可求出实数a的取值范围;
在[1,+∞)上恒成立,求右边函数的最大值,即可求出实数a的取值范围;(Ⅲ)g(x)=x2f'(x)=2x3+ax-2,g′(x)=6x2+a,分类讨论求出函数的最小值点.利用g(x)的最小值是-6,可求函数f(x)的解析式.
点评:本题以函数为载体,考查导数的运用,考查利用导数求函数的单调区间,考查函数的最值,考查学生等价转化问题的能力.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目

 ,求f(x)的解析式.
,求f(x)的解析式.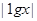 ,若a < b,且f(a) = f(b),则a + 2b的取值范围是________ .
,若a < b,且f(a) = f(b),则a + 2b的取值范围是________ .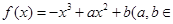 R).
R).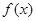 的图象能否总在直线
的图象能否总在直线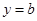 的下方?说明理由;
的下方?说明理由;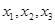 为方程
为方程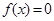 的三个根,且
的三个根,且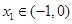 ,
,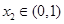 ,
,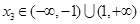 , 求证:
, 求证: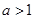 或
或