题目内容
10.在直角坐标系xOy中,以原点O为圆心作一个单位圆,角α和角β的终边与单位圆分别交于A、B两点,且|$\overrightarrow{AB}$|=$\frac{{2\sqrt{5}}}{5}$.若0<α<$\frac{π}{2}$,-$\frac{π}{2}$<β<0,sinβ=-$\frac{5}{13}$.(1)求△AOB的面积;
(2)求sinα的值.
分析 (1)根据题意设出$\overrightarrow{OA}$,$\overrightarrow{OB}$,利用向量法则根据$\overrightarrow{OB}$-$\overrightarrow{OA}$表示出$\overrightarrow{AB}$,利用向量模的定义列出关系式,整理后利用两角和与差的余弦函数公式即可求出cos(α-β)的值,由α与β的范围求出α-β的范围,利用同角三角函数间的基本关系求出sin(α-β),由三角形面积公式即可得解.
(2)可先求cosβ的值,所求式子变形后,利用两角和与差的正弦函数公式化简,将各自的值代入计算即可求出值.
解答 解:(1)根据题意设$\overrightarrow{OA}$=(cosα,sinα),$\overrightarrow{OB}$=(cosβ,sinβ),
∴$\overrightarrow{AB}$=$\overrightarrow{OB}$-$\overrightarrow{OA}$=(cosβ-cosα,sinβ-sinα),
∴|$\overrightarrow{AB}$|2=(cosβ-cosα)2+(sinβ-sinα)2=$\frac{4}{5}$,即2-2(cosβcosα+sinβsinα)=$\frac{4}{5}$,
∴cos(α-β)=cosβcosα+sinβsinα=$\frac{3}{5}$;
∵0<α<$\frac{π}{2}$,-$\frac{π}{2}$<β<0,
∴0<α-β<π,
∴sin∠AOB=sin(α-β)=$\sqrt{1-co{s}^{2}(α-β)}$=$\frac{4}{5}$,
又∵|OA|=1,|OB|=1,
∴S△AOB=$\frac{1}{2}$|OA|•|OB|sin∠AOB=$\frac{1}{2}×1×1×\frac{4}{5}$=$\frac{2}{5}$.
(2)∵sinβ=-$\frac{5}{13}$,
∴cosβ=$\sqrt{1-si{n}^{2}β}$=$\frac{12}{13}$,
则sinα=sin[(α-β)+β]=sin(α-β)cosβ+cos(α-β)sinβ=$\frac{4}{5}$×$\frac{12}{13}$-$\frac{3}{5}$×$\frac{5}{13}$=$\frac{33}{65}$.
点评 此题考查了两角和与差的余弦函数公式,以及同角三角函数间的基本关系,考查了平面向量的运算,熟练掌握公式是解本题的关键,属于中档题.

 名校课堂系列答案
名校课堂系列答案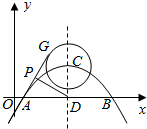 已知抛物线$y=-\frac{3}{16}(x-1)(x-9)$与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则DP的最大值为( )
已知抛物线$y=-\frac{3}{16}(x-1)(x-9)$与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则DP的最大值为( )| A. | $\frac{7}{2}$ | B. | $\frac{{\sqrt{41}}}{2}$ | C. | $\frac{{\sqrt{34}}}{2}$ | D. | $2\sqrt{3}$ |
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
| A. | {x|x<-2或x≥0} | B. | {x|x<-2或x>1} | C. | {x|x<-4或x≥0} | D. | {x|x<-4或x>1} |
 已知函数f(x)=x-|x-1|,$g(x)={(\frac{1}{2})^{x-1}}$.
已知函数f(x)=x-|x-1|,$g(x)={(\frac{1}{2})^{x-1}}$.