题目内容
在△ABC中，角A，B，C的对边分别为a，b，c，若点（a，b）在直线x（sinA+sinB）+ysinB=csinC上，则角C的值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：将（a，b）代入直线解析式，再利用正弦定理化简，利用余弦定理表示出cosC，将得出的关系式代入求出cosC的值，即可确定出C的度数．
解答：
解：将（a，b）代入直线解析式得：a（sinA+sinB）+bsinB=csinC，
利用正弦定理化简得：a（a+b）+b2=c2，即a2+b2-c2=-ab，
∴cosC=
=-
，
则C=
．
故选：C．
利用正弦定理化简得：a（a+b）+b2=c2，即a2+b2-c2=-ab，
∴cosC=
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
则C=
| 2π |
| 3 |
故选：C．
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
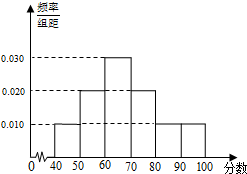某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生的成绩进行统计，得到如图所示的样本频率分布直方图．若规定60分及以上为合格，则估计这1000名学生中合格人数是
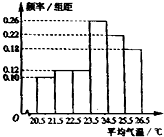如图是根据部分城市某年6月份的平均气温（单位：℃）数据得到的样本频率分布直方图，其中平均气温的范围是[20.5，26.5]，样本数据的分组为[20.5，21.5），[21.5，22.5），[22.5，23.5），[23.5，24.5），[24.5，25.5），[25.5，26.5]．已知样本中平均气温低于22.5℃的城市个数为11，则样本中平均气温不低于25.5℃的城市个数为（ ）已知a=2ln3，b=2lg2，c=（
） log
，则（ ）
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、c＞a＞b |
| B、a＞b＞c |
| C、a＞c＞b |
| D、b＞c＞a |
等差数列{an}中，a2=2007，a9=a5-12，则其前n项和Sn取最大值时n等于（ ）
| A、670 |
| B、671 |
| C、670或671 |
| D、671或672 |
已知a＞0，b＞0，且H=max{
，
}，其中maxA表示数集A中的最大数．则下列结论中正确的是（ ）
| 1 |
| a |
| a2+b2 |
| b |
A、H有最大值
| ||||
B、H有最小值
| ||||
C、H有最小值
| ||||
D、H有最大值
|