题目内容
已知函数m(x)=2ax2, ,且函数h(x)在
,且函数h(x)在 时取极大值,若f(x)=h(x)+m(x)
时取极大值,若f(x)=h(x)+m(x)
(1)当 时,求函数f(x)在[-2,2]上的最大值和最小值;
时,求函数f(x)在[-2,2]上的最大值和最小值;
(2)令g(x)=ln(x+1)+3-f'(x),若g(x)在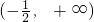 上单调递增,求实数a的取值范围.
上单调递增,求实数a的取值范围.
解:(1)函数 求导可得:h′(x)=-2x2+b
求导可得:h′(x)=-2x2+b
∵函数h(x)在 时取极大值,
时取极大值,
∴
∴b=3
∴
∴f(x)=h(x)+m(x)=
当 时,f(x)=
时,f(x)=
∴f′(x)=-(2x-3)(x+1)
令f′(x)>0,-2≤x≤2,可得-1<x< ;令f′(x)<0,-2≤x≤2,可得
;令f′(x)<0,-2≤x≤2,可得 <x≤2或-2≤x<-1;
<x≤2或-2≤x<-1;
∴当x=-1时,f(x)极小值,当 时,f(x)取极大值(6分)
时,f(x)取极大值(6分)
而

∴在[-2,2]上,当x=-1时, ;当
;当 时,
时, (7分)
(7分)
(2)g(x)=ln(x+1)+3-f′(x)=ln(x+1)+3-(-2x2+3+4ax)=ln(x+1)+2x2-4ax
求导函数,可得 (8分)
(8分)
在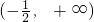 上,x+1>0
上,x+1>0
∵g(x)在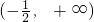 单调递增.
单调递增.
∴g′(x)>0,∴ ,即
,即
∴
∵在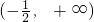 上,
上,
∴a≤0
∴实数a的取值范围a≤0
分析:(1)根据函数h(x)在 时取极大值,可求得
时取极大值,可求得 ,从而可得当
,从而可得当 时,f(x)=
时,f(x)= ,求导函数,确定函数的单调性,求出函数的极值与端点函数值比较,即可得到函数的最大值和最小值;
,求导函数,确定函数的单调性,求出函数的极值与端点函数值比较,即可得到函数的最大值和最小值;
(2)g(x)=ln(x+1)+3-f′(x)=ln(x+1)+3-(-2x2+3+4ax)=ln(x+1)+2x2-4ax,求导函数,利用g(x)在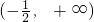 单调递增,可得
单调递增,可得 ,根据在
,根据在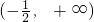 上,
上, ,即可求得实数a的取值范围.
,即可求得实数a的取值范围.
点评:本题考查导数知识的运用,考查函数的单调性、极值与最值,考查恒成立问题,解题的关键是分离参数,属于中档题.
 求导可得:h′(x)=-2x2+b
求导可得:h′(x)=-2x2+b∵函数h(x)在
 时取极大值,
时取极大值,∴

∴b=3
∴

∴f(x)=h(x)+m(x)=

当
 时,f(x)=
时,f(x)=
∴f′(x)=-(2x-3)(x+1)
令f′(x)>0,-2≤x≤2,可得-1<x<
 ;令f′(x)<0,-2≤x≤2,可得
;令f′(x)<0,-2≤x≤2,可得 <x≤2或-2≤x<-1;
<x≤2或-2≤x<-1;∴当x=-1时,f(x)极小值,当
 时,f(x)取极大值(6分)
时,f(x)取极大值(6分)而


∴在[-2,2]上,当x=-1时,
 ;当
;当 时,
时, (7分)
(7分)(2)g(x)=ln(x+1)+3-f′(x)=ln(x+1)+3-(-2x2+3+4ax)=ln(x+1)+2x2-4ax
求导函数,可得
 (8分)
(8分)在
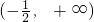 上,x+1>0
上,x+1>0∵g(x)在
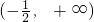 单调递增.
单调递增.∴g′(x)>0,∴
 ,即
,即
∴

∵在
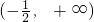 上,
上,
∴a≤0
∴实数a的取值范围a≤0
分析:(1)根据函数h(x)在
 时取极大值,可求得
时取极大值,可求得 ,从而可得当
,从而可得当 时,f(x)=
时,f(x)= ,求导函数,确定函数的单调性,求出函数的极值与端点函数值比较,即可得到函数的最大值和最小值;
,求导函数,确定函数的单调性,求出函数的极值与端点函数值比较,即可得到函数的最大值和最小值;(2)g(x)=ln(x+1)+3-f′(x)=ln(x+1)+3-(-2x2+3+4ax)=ln(x+1)+2x2-4ax,求导函数,利用g(x)在
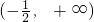 单调递增,可得
单调递增,可得 ,根据在
,根据在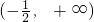 上,
上, ,即可求得实数a的取值范围.
,即可求得实数a的取值范围.点评:本题考查导数知识的运用,考查函数的单调性、极值与最值,考查恒成立问题,解题的关键是分离参数,属于中档题.

练习册系列答案
相关题目