题目内容
19.已知$f(α)=\frac{{sin(α-\frac{π}{2})cos(\frac{3π}{2}-α)tan(π+α)cos(\frac{π}{2}+α)}}{sin(2π-α)tan(-α-π)sin(-α-π)}$.(1)化简f(α);
(2)若$α=-\frac{31π}{3}$,求f(α)的值.
分析 (1)由条件利用诱导公式化简所给的三角函数式,可得结果.
(2)由条件利用诱导公式化简所给的三角函数式,可得f(α)的值.
解答 解:(1)$f(α)=\frac{-cosα(-sinα)tanα(-sinα)}{-sinα(-tanα)sinα}=-cosα$.
(2)因为$-\frac{31π}{3}=-5×2π-\frac{π}{3}$,
∴$f({-\frac{31π}{3}})=-cos(-\frac{31π}{3})=-cos(-5×2π-\frac{π}{3})=-cos\frac{π}{3}=-\frac{1}{2}$,
即 $f(α)=-\frac{1}{2}$.
点评 本题主要考查利用诱导公式进行化简求值,属于基础题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
4.x∈[0,2π],$y=\sqrt{tanx}+\sqrt{-cosx}$定义域为( )
| A. | $x∈[0,\frac{π}{2})$ | B. | $(\frac{π}{2},π]$ | C. | $[π,\frac{3π}{2})$ | D. | $(\frac{3π}{2},2π]$ |
8.阅读如图所示的程序框图,运行相应的程序,输出的S=( )
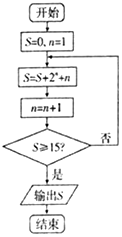

| A. | 40 | B. | 21 | C. | 20 | D. | 18 |
 一辆汽车由A地开往B地,它距离B地的路程s(km)与行驶时间t(h)的关系如图所示,如果汽车一直快速行驶,那么可以提前2小时到达B地.
一辆汽车由A地开往B地,它距离B地的路程s(km)与行驶时间t(h)的关系如图所示,如果汽车一直快速行驶,那么可以提前2小时到达B地.