题目内容
设椭圆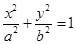 (a>b>0)的两焦点为F1、F2,若椭圆上存在一点Q,使∠F1QF2=120º,椭圆离心率e的取值范围为( )
(a>b>0)的两焦点为F1、F2,若椭圆上存在一点Q,使∠F1QF2=120º,椭圆离心率e的取值范围为( )
A.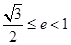 | B.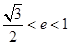 | C.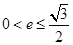 | D.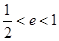 |
A
解析试题分析:设Q(x1,y1),F1(-c,0),F2(c,0),c>0,则|QF1|=a+ex1,|QF2|=a-ex1.在△QF1F2中,由余弦定理得 cos120°=- =
= ,解得 x12=
,解得 x12= .∵x12∈(0,a2],∴0≤
.∵x12∈(0,a2],∴0≤ <a2,即4c2-3a2≥0.且e2<1,∴e=
<a2,即4c2-3a2≥0.且e2<1,∴e= ≥
≥ .故椭圆离心率的取范围是 e∈[
.故椭圆离心率的取范围是 e∈[ , 1).故选A
, 1).故选A
考点:本题考查了椭圆的应用
点评:当Q点在短轴的端点时∠F1QF2值最大,这个结论可以记住它.在做选择题和填空题的时候直接拿来解决这一类的问题

练习册系列答案
相关题目
若抛物线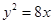 上一点
上一点 到其焦点的距离为
到其焦点的距离为 ,则点
,则点 的坐标为( )
的坐标为( )
A.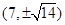 | B. | C. | D. |
双曲线 的实轴长是( )
的实轴长是( )
| A.2 | B.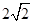 | C.4 | D.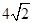 |
若点 到双曲线
到双曲线
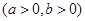 的一条渐近线的距离为
的一条渐近线的距离为 ,则该双曲线的离心率为
,则该双曲线的离心率为
A. | B. | C. | D. |
已知抛物线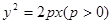 与双曲线
与双曲线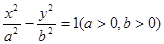 有相同的焦点
有相同的焦点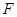 ,点
,点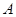 是两曲线的交点,且
是两曲线的交点,且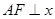 轴,则双曲线的离心率为( )
轴,则双曲线的离心率为( )
A.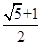 | B.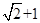 | C.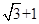 | D.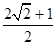 |
 右支上一点,F1、F2分别为双曲线的左、右焦点,I为
右支上一点,F1、F2分别为双曲线的左、右焦点,I为 的内心,若
的内心,若 成立,则
成立,则 的值为 ( )
的值为 ( )



 上,那么点P到点Q(2,1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
上,那么点P到点Q(2,1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
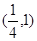


 的右焦点
的右焦点 作圆
作圆 的切线
的切线 (切点为
(切点为 ),交
),交 轴于点
轴于点 .若
.若 的中点,则双曲线的离心率为
的中点,则双曲线的离心率为


 在抛物线
在抛物线 上,那么
上,那么 的距离与点
的距离与点


