题目内容
已知f（x）是奇函数，且图象与x轴有交点，则方程f（x）=0的所有实根的和是（ ）
| A、0 | B、1 | C、0 | D、4 |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：由函数y=f（x）是奇函数，知其图象关于原点轴对称，与x轴的自然也关于原点对称可得结论．
解答：
解：∵函数y=f（x）是奇函数
∴其图象关于原点对称
∴其图象与x轴的交点也关于原点对称
∴方程f（x）=0 的所有实根之和为0
故选：A
∴其图象关于原点对称
∴其图象与x轴的交点也关于原点对称
∴方程f（x）=0 的所有实根之和为0
故选：A
点评：本题主要考查奇函数的图象关于原点对称，同时考查函数与方程的转化．
练习册系列答案
相关题目
在下面的程序框图中，若输入的a，b，c分别为9，-10，0，则输出的a的值为（ ）
| A、0 | B、9 |
| C、-10 | D、以上均不是 |
函数f （x）=|2x-a|+1 的定义域为[p，q]，值域为[1，2]，则q-p的最大值为（ ）
| A、1 | B、2 |
| C、a+1 | D、2 a |
已知函数f（x）=ax2+2ax+5（0＜a＜3），若x1＜x2，x1+x2=1-a，则（ ）
| A、f（x1）＞f（x2） |
| B、f（x1）＜f（x2） |
| C、f（x1）=f（x2） |
| D、f（x1）与f（x2）的大小不能确定 |
从3名男生和2名女生中选出3名代表去参加辩论比赛，则所选出的3名代表中至少有1名女生的选法共有（ ）
| A、9种 | B、10种 |
| C、12种 | D、20种 |
掷一枚质地均匀的硬币3次，恰有2次正面向上的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知数列{an}满足a1＞0，且an+1=
an，则数列{an}是（ ）
| 1 |
| 2 |
| A、递增数列 | B、递减数列 |
| C、常数列 | D、摆动数列 |
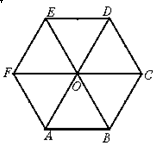如图，设O是正六边形ABCDEF的中心，在向量| OB |
| OC |
| OD |
| OE |
| OF |
| AB |
| BC |
| CD |
| EF |
| DE |
| FA |
| OA |
| A、1个 | B、2个 | C、3个 | D、4个 |