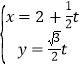题目内容
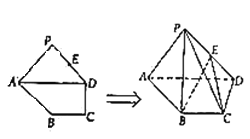
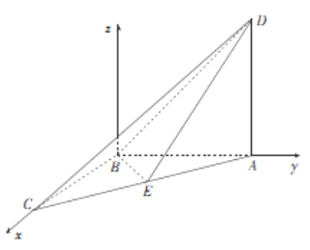
【题目】如图所示,在四面体![]() 中,
中,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,且
,且![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)设![]() 为棱
为棱![]() 的中点,当四面体
的中点,当四面体![]() 的体积取得最大值时,求二面角
的体积取得最大值时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)根据面面垂直的性质得到![]() 平面
平面![]() ,从而得到
,从而得到![]() ,利用勾股定理得到
,利用勾股定理得到![]() ,利用线面垂直的判定定理证得
,利用线面垂直的判定定理证得![]() 平面
平面![]() ;
;
(2)设![]() ,利用椎体的体积公式求得
,利用椎体的体积公式求得![]()
![]()
![]() ,利用导数研究函数的单调性,从而求得
,利用导数研究函数的单调性,从而求得![]() 时,四面体
时,四面体![]() 的体积取得最大值,之后利用空间向量求得二面角的余弦值.
的体积取得最大值,之后利用空间向量求得二面角的余弦值.
(1)证明:因为![]() ,平面
,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
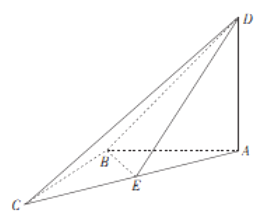
(2)解:设![]() ,则
,则![]() ,
,
四面体![]() 的体积
的体积![]()
![]()
![]() .
.
![]()
![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
故当![]() 时,四面体
时,四面体![]() 的体积取得最大值.
的体积取得最大值.
以![]() 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则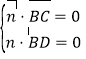 ,即
,即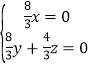 ,
,
令![]() ,得
,得![]() ,
,
同理可得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() .
.
由图可知,二面角![]() 为锐角,故二面角
为锐角,故二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目