题目内容
8.$\frac{{2-5{i^{2015}}}}{{1+3{i^{2013}}}}$=( )| A. | $\frac{3}{10}+\frac{9}{10}$i | B. | $\frac{3}{10}-\frac{9}{10}i$ | C. | $-\frac{3}{10}+\frac{9}{10}i$ | D. | $\frac{17}{10}-\frac{1}{10}$i |
分析 由于i4=1,可得i2013=(i4)503•i=i,i2015=-i,再利用复数的运算法则即可得出.
解答 解:∵i4=1,∴i2013=(i4)503•i=i,i2015=(i4)503•i3=-i,
∴原式=$\frac{2-5(-i)}{1+3i}$=$\frac{(2+5i)(1-3i)}{(1+3i)(1-3i)}$=$\frac{17-i}{10}$,
故选:D.
点评 本题考查了复数的运算法则、周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知公共汽车每7min一班,在车站停留1min,开走后再过7min第二辆车到站,则乘客到达车站立即可以上车的概率为( )
| A. | $\frac{1}{7}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{9}$ |
5.已知函数f(x)=x3-3x-1,g(x)=2x-a,若对任意x1∈[0,2],存在x2∈[0,2]使|f(x1)-g(x2)|≤2,则实数a的取值范围( )
| A. | [1,5] | B. | [2,5] | C. | [-2,2] | D. | [5,9] |
3.设变量x、y满足约束条件$\left\{{\begin{array}{l}{x-y≥0}\\{x+y≤1}\\{x+2y≥1}\end{array}}\right.$,则z=32x-y的最大值为( )
| A. | $\root{3}{3}$ | B. | $\sqrt{3}$ | C. | 3 | D. | 9 |
20.已知命题p1:函数y=ex-e-x在R上为增函数;命题p2:函数y=ex+e-x在R上为减函数,则在命题q1:p1∨p2,q2:p1∧p2,q3:(¬p1)∨p2,q4:p1∧(¬p2)中,真命题是( )
| A. | q1、q3 | B. | q2、q3 | C. | q1、q4 | D. | q2、q4 |
17.已知菱形ABCD的边长为2,∠BAD=120°,点E、F分别在边BC、CD上,$\overrightarrow{BE}$=λ$\overrightarrow{BC}$,$\overrightarrow{DF}$=μ$\overrightarrow{DC}$.若λ+μ=$\frac{2}{3}$,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的最小值( )
| A. | $\frac{4}{9}$ | B. | $\frac{5}{9}$ | C. | $\frac{10}{9}$ | D. | $\frac{11}{9}$ |
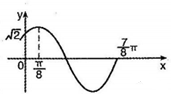 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则此函数的解析式为f(x)=2sin(2x+$\frac{π}{4}$).
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则此函数的解析式为f(x)=2sin(2x+$\frac{π}{4}$).