题目内容
3.设变量x、y满足约束条件$\left\{{\begin{array}{l}{x-y≥0}\\{x+y≤1}\\{x+2y≥1}\end{array}}\right.$,则z=32x-y的最大值为( )| A. | $\root{3}{3}$ | B. | $\sqrt{3}$ | C. | 3 | D. | 9 |
分析 首先由约束条件画出可行域,令2x-y=t,利用t的几何意义求出最值,然后求z 的最值.
解答 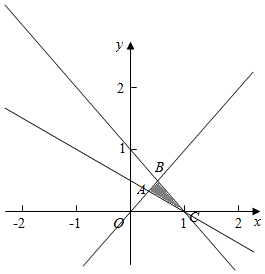 解:约束条件对应的平面区域如图:
解:约束条件对应的平面区域如图:
令2x-y=t,变形得y=2x-t,根据t的几何意义,由约束条件知t过A时在y轴的截距最大,使t最小,由$\left\{\begin{array}{l}{x-y=0}\\{x+2y=1}\end{array}\right.$得到交点A($\frac{1}{3}$,$\frac{1}{3}$)所以t最小为$\frac{1}{3}×1-\frac{1}{3}=\frac{1}{3}$;过C时直线y=2x-t在y轴截距最小,t最大,由$\left\{\begin{array}{l}{x+y=1}\\{x+2y=1}\end{array}\right.$解得C(1,0),所以t的最大值为2×1-0=2,所以$t∈[\frac{1}{3},2]$,故${z_{max}}={3^2}=9$;
故选D.
点评 本题考查了简单线性规划问题;利用数形结合的方法,借助于目标函数的几何意义求最值.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
2.从1,2,3,4,5中挑出三个不同数字组成五位数,则其中有两个数字各用两次(例如,12332)的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
3.已知数列{an}是等比数列且数列{|an|}是递增数列,a2+a3=2,a1a4=-8,则a2016=( )
| A. | $\frac{1}{{2}^{2015}}$ | B. | -$\frac{1}{{2}^{2015}}$ | C. | -22015 | D. | 22015 |
8.$\frac{{2-5{i^{2015}}}}{{1+3{i^{2013}}}}$=( )
| A. | $\frac{3}{10}+\frac{9}{10}$i | B. | $\frac{3}{10}-\frac{9}{10}i$ | C. | $-\frac{3}{10}+\frac{9}{10}i$ | D. | $\frac{17}{10}-\frac{1}{10}$i |
13.已知i为虚数单位,则复数$\frac{i}{2-i}$等于( )
| A. | -$\frac{1}{5}$+$\frac{2}{5}$i | B. | $\frac{1}{5}$-$\frac{2}{5}$i | C. | -$\frac{2}{5}$+$\frac{1}{5}$i | D. | $\frac{2}{5}$-$\frac{1}{5}$i |