题目内容
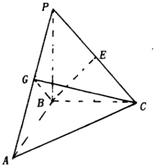 (2012•泰安一模)在三棱锥P-ABC中,PB⊥平面ABC,AB⊥BC,AB=PB=2,BC=2
(2012•泰安一模)在三棱锥P-ABC中,PB⊥平面ABC,AB⊥BC,AB=PB=2,BC=2| 3 |
(I)求证:平面BCG⊥平面PAC;
(II)在线段AC上是否存在一点N,使PN⊥BE?证明你的结论.
分析:(1)由题意可证BC⊥平面PAB,从而证得PA⊥BC,又Rt△PAB为等腰直角三角形,故BG⊥PA,从而得PA⊥平面BCG,结论可证;
(2)以点B为坐标原点,BA为x轴,BC为y轴,BP为z轴建立空间直角坐标系,可求得E点,N点的坐标,从而得
=(0,
,1),
=(x0,
-
x0,-2),由空间向量的坐标运算
•
=0即可得到答案.
(2)以点B为坐标原点,BA为x轴,BC为y轴,BP为z轴建立空间直角坐标系,可求得E点,N点的坐标,从而得
| BE |
| ||
| 2 |
| PN |
| 3 |
| ||
| 2 |
| BE |
| PN |
解答: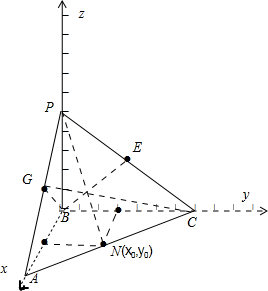 解:(Ⅰ)∵PB⊥平面ABC,BC?平面ABC,
解:(Ⅰ)∵PB⊥平面ABC,BC?平面ABC,
∴BC⊥PB,
又AB⊥BC,AB∩BP=B,
∴BC⊥平面PAB,PA?平面PAB,
∴BC⊥PA.①
又AB=PB=2,△PAB为等腰直角三角形,G为斜边PA的中点,
∴BG⊥PA,②又BG∩BC=B,
∴PA⊥平面BCG,PA?平面PAC,
∴平面BCG⊥平面PAC;
(Ⅱ)以点B为坐标原点,BA为x轴,BC为y轴,BP为z轴建立空间直角坐标系,则A(2,0,0),C(0,2
,0),P(0,0,2),E(0,
,1),
设存在点N∈AC,使PN⊥BE,点N的坐标设为:N(x0,y0,0)
则:得
=(0,
,1),
=(x0,y0,-2)
由相似三角形得:
=
,即
=
,
∴y0=2
-
x0.
∴
=(x0,2
-
x0,-2)
又PN⊥BE,
∴
•
=0.
∴0×x0+
×(2
-
x0)+1×(-2)=0,
∴x0=
∈[0,2]
故存在点N∈AC,使PN⊥BE.
 解:(Ⅰ)∵PB⊥平面ABC,BC?平面ABC,
解:(Ⅰ)∵PB⊥平面ABC,BC?平面ABC,∴BC⊥PB,
又AB⊥BC,AB∩BP=B,
∴BC⊥平面PAB,PA?平面PAB,
∴BC⊥PA.①
又AB=PB=2,△PAB为等腰直角三角形,G为斜边PA的中点,
∴BG⊥PA,②又BG∩BC=B,
∴PA⊥平面BCG,PA?平面PAC,
∴平面BCG⊥平面PAC;
(Ⅱ)以点B为坐标原点,BA为x轴,BC为y轴,BP为z轴建立空间直角坐标系,则A(2,0,0),C(0,2
| 3 |
| 3 |
设存在点N∈AC,使PN⊥BE,点N的坐标设为:N(x0,y0,0)
则:得
| BE |
| 3 |
| PN |
由相似三角形得:
| 2-x0 |
| |AB| |
| y0 |
| |BC| |
| 2-x0 |
| 2 |
| y0 | ||
2
|
∴y0=2
| 3 |
| 3 |
∴
| PN |
| 3 |
| 3 |
又PN⊥BE,
∴
| BE |
| PN |
∴0×x0+
| 3 |
| 3 |
| 3 |
∴x0=
| 4 |
| 3 |
故存在点N∈AC,使PN⊥BE.
点评:本题考查平面与平面垂直的判定,考查空间中直线与直线之间的位置关系,突出考查向量法的应用,属于中档题.

练习册系列答案
相关题目
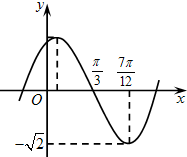 (2012•泰安一模)函数f(x)=Asin(ωx+?)(A,ω,?为常数,A>0,ω>0)的部分图象如图所示,则
(2012•泰安一模)函数f(x)=Asin(ωx+?)(A,ω,?为常数,A>0,ω>0)的部分图象如图所示,则