题目内容
如图,在四棱柱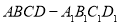 中,底面
中,底面 是等腰梯形,
是等腰梯形,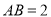 ,
,
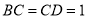
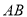 ∥
∥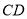 ,顶点
,顶点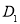 在底面
在底面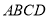 内的射影恰为点
内的射影恰为点 .
.

(Ⅰ)求证: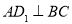 ;
;
(Ⅱ)在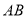 上是否存在点
上是否存在点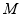 ,使得
,使得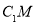 ∥平面
∥平面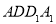 ?若存在,确定点
?若存在,确定点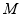 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(1)证明见解析;(2)存在点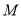 是
是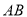 的中点,证明见解析.
的中点,证明见解析.
【解析】
试题分析:(1)解决立体几何的有关问题,空间想象能力是非常重要的,但新旧知识的迁移融合也很重要,在平面几何的基础上,把某些空间问题转化为平面问题来解决,有时很方便;(2)证明线线垂直时,要注意题中隐含的垂直关系,如等腰三角形的底边上的高,中线和顶角的角平分线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形等等;(3)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质.
试题解析:(Ⅰ)证明:连接 ,则
,则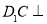 平面
平面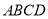 ,
,
∴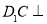
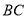
在等腰梯形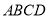 中,连接
中,连接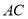
∵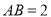 ,
,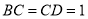 ,
,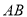 ∥
∥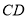
∴
∴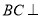 平面
平面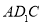
∴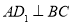 6分
6分
(Ⅱ)设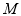 是
是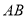 上的点
上的点
∵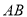 ∥
∥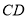 ∴
∴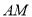 ∥
∥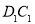
因经过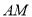 、
、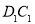 的平面与平面
的平面与平面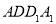 相交与
相交与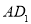 ,要是
,要是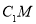 ∥平面
∥平面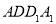 ,则
,则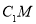 ∥
∥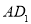 ,即四边形
,即四边形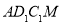 为平行四边形 ,此时
为平行四边形 ,此时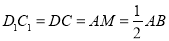 ,即点
,即点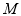 为
为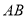 的中点.
的中点.
所以在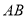 上存在点
上存在点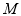 ,使得
,使得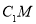 ∥平面
∥平面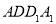 ,此时点
,此时点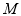 为
为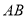 的中点. 12分
的中点. 12分
考点:1、直线与直线垂直的判定;2、直线与平面平行的判定.
考点分析: 考点1:点、线、面之间的位置关系 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
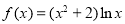 ,
,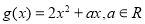
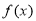 是
是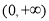 上的增函数;
上的增函数;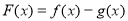 ,当
,当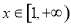 时,
时,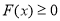 恒成立,求
恒成立,求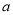 的取值范围.
的取值范围. 中,
中, ,
, ,
, ,则( )
,则( ) 或
或 B.
B. C.
C. D.以上答案都不对
D.以上答案都不对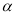 ,
,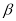 ,
,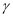 为平面,
为平面,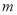 ,
,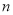 为直线,则
为直线,则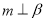 的一个充分条件是( )
的一个充分条件是( )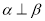 ,
,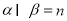 ,
,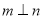 B.
B.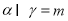 ,
, ,
,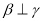
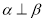 ,
,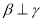 ,
,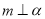 D.
D.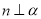 ,
,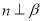 ,
,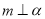
 中,曲线
中,曲线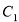 的参数方程为
的参数方程为 ,(
,(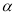 为参数),以原点
为参数),以原点 为极点,
为极点,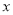 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线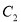 的极坐标方程为
的极坐标方程为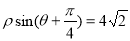 .
.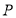 为曲线
为曲线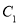 上的动点,求点
上的动点,求点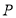 到
到 ,
, ,则
,则 .
.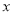 的值是
的值是
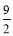 C.
C.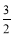 D.3
D.3 ,
, ,则
,则 .
. 的对称中心为原点
的对称中心为原点 ,焦点在
,焦点在 轴上,左右焦点分别为
轴上,左右焦点分别为 和
和 ,且
,且 ,点
,点 在该椭圆上.
在该椭圆上. 的方程;
的方程; 的直线
的直线 与椭圆
与椭圆 相交于
相交于 两点,若
两点,若 的面积为
的面积为 ,求以
,求以 为圆心且与直线
为圆心且与直线