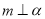题目内容
已知函数 ,若方程
,若方程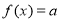 有四个不同的解
有四个不同的解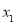 ,
,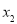 ,
,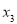 ,
,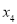 ,且
,且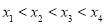 ,则
,则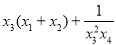 的取值范围是( )
的取值范围是( )
A.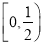 B.
B.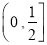 C.
C.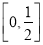 D.
D.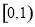
B
【解析】
试题分析:先画出函数 ,的图象,方程
,的图象,方程 有四个不同的解
有四个不同的解 ,
, ,
, ,
, ,且
,且 ,由
,由 时,
时, ,则横坐标为
,则横坐标为 与
与 两点的中点横坐标为
两点的中点横坐标为
即: ,当
,当 时,由于
时,由于 在
在 上是减函数,在
上是减函数,在 上是增函数,又因为
上是增函数,又因为 ,
, ,则
,则 ,有
,有 ,
,


 ,因为
,因为 满足
满足 ,设
,设 ,
,
因为
 ,
, 在
在 上是减函数,则
上是减函数,则 ,则
,则


 ,选
,选 .(说明:求
.(说明:求 的范围也可直接使用对勾函数)
的范围也可直接使用对勾函数)

考点:1.含绝对值符号的函数;2.对数函数;3.用导数研究函数的值域;
考点分析: 考点1:函数与方程 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
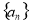 的前
的前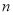 项和为
项和为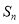 ,且满足
,且满足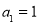 ,
, 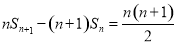 ,
, 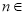 N
N .
.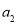 的值;
的值;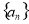 的通项公式;
的通项公式;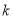 ,使
,使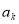 ,
, ,
, 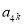 成等比数列? 若存在,求
成等比数列? 若存在,求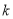 的值; 若不存在,请说明理由.
的值; 若不存在,请说明理由. ,若
,若 ,则实数
,则实数 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 中,内角
中,内角 所对的边分别为
所对的边分别为 ,若
,若 .
. 成等比数列;(2)若
成等比数列;(2)若 ,求
,求 的面积
的面积 .
.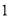 的等边
的等边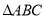 中,
中,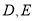 分别在边BC与AC上,且
分别在边BC与AC上,且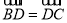 ,
,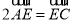
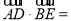 ( )
( )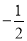 B.
B. 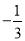 C.
C.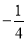 D.
D.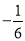
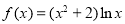 ,
,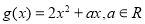
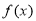 是
是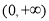 上的增函数;
上的增函数;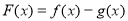 ,当
,当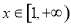 时,
时,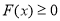 恒成立,求
恒成立,求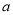 的取值范围.
的取值范围.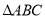 中“
中“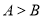 ”是“
”是“ ”的( )
”的( )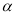 ,
,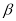 ,
,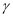 为平面,
为平面,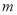 ,
,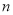 为直线,则
为直线,则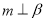 的一个充分条件是( )
的一个充分条件是( )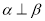 ,
,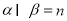 ,
,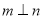 B.
B.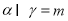 ,
, ,
,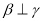
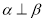 ,
,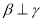 ,
,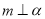 D.
D.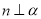 ,
,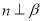 ,
,