Question

9．如图，平面PBA⊥平面ABCD，∠DAB=90°，PB=AB，BF⊥PA，点E在线段AD上移动．
（Ⅰ）当点E为AD的中点时，求证：EF∥平面PBD；
（Ⅱ）求证：无论点E在线段AD的何处，总有PE⊥BF．

Answer 1

分析 （Ⅰ）由已知可证F是PA的中点，连接EF，由中位线的性质可得EF∥PD，又EF?平面PBD，PD?平面PBD，由判定定理即可证明EF∥平面PBD．
（Ⅱ）只要证明DA⊥BF，BF⊥PA，从而证明BF⊥面PDA，又PE?平面PDA，所以无论点E在线段AD的何处，总有PE⊥BF．

解答 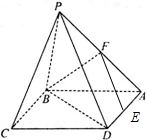证明：（Ⅰ）因为在三角形PBA中，PB=AB，BF⊥PA，
所以F是PA的中点，连接EF，…（2分）
在△PDA中，点E，F分别是边AD，PA的中点，
所以EF∥PD…（4分）
又EF?平面PBD，PD?平面PBD
所以EF∥平面PBD．…（6分）
（Ⅱ）因为平面PBA⊥平面ABCD，平面PBA∩平面ABCD=AB，∠DAB=90°，DA⊥AB，DA?平面ABCD
所以DA⊥平面PBA…（8分）
又BF?平面PBA，所以DA⊥BF，又BF⊥PA，PA∩DA=A，PA，DA?平面PDA，
所以BF⊥面PDA…（10分）
又PE?平面PDA所以BF⊥PE
所以无论点E在线段AD的何处，总有PE⊥BF．…（12分）

点评 本题主要考查了直线与平面平行的判定，直线与平面垂直的性质，考查了空间想象能力和转化思想，属于基本知识的考查．