题目内容
10.已知椭圆C的长轴左、右顶点分别为A,B,离心率e=$\frac{\sqrt{2}}{2}$,右焦点为F,且$\overrightarrow{AF}$$•\overrightarrow{BF}$=-1.(1)求椭圆C的标准方程:
(2)若P是椭圆C上的一动点,点P关于坐标原点的对称点为Q,点P在x轴上的射影点为M,连接QM并延长交椭圆于点N.求证:∠QPN=90°.
分析 (1)由已知得到A,B,F的坐标,结合$\overrightarrow{AF}$$•\overrightarrow{BF}$=-1,离心率为$\frac{\sqrt{2}}{2}$,以及隐含条件得到关于a,b,c的方程组,求解方程组得到a,b的值,则椭圆的方程可求;
(2)设P(x0,y0),则Q(-x0,-y0),M(x0,0),由直线方程的两点式写出QM所在直线方程,和椭圆方程联立求出N的坐标,进一步求得QP,PN所在直线斜率,由斜率之积等于-1可得答案.
解答 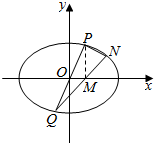 (1)解:由题意可知:A(-a,0),B(a,0),F(c,0),
(1)解:由题意可知:A(-a,0),B(a,0),F(c,0),
∵$\overrightarrow{AF}$$•\overrightarrow{BF}$=-1,∴(c+a,0)•(c-a,0)=c2-a2=-1,
又∵e=$\frac{c}{a}=\frac{\sqrt{2}}{2}$,a2=b2+c2,
联立解得b2=1,a2=2,c2=1.
∴椭圆的标准方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)证明:设P(x0,y0),则Q(-x0,-y0),M(x0,0),
∴QM所在直线方程为$\frac{y}{-{y}_{0}}=\frac{x-{x}_{0}}{-2{x}_{0}}$,即$y=\frac{{y}_{0}}{2{x}_{0}}(x-{x}_{0})$,
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}+{y}^{2}=1}\\{y=\frac{{y}_{0}}{2{x}_{0}}(x-{x}_{0})}\end{array}\right.$,解得N($\frac{2{{x}_{0}}^{3}+3{x}_{0}{{y}_{0}}^{2}}{2{{x}_{0}}^{2}+{{y}_{0}}^{2}}$,$\frac{{{y}_{0}}^{3}}{2{{x}_{0}}^{2}+{{y}_{0}}^{2}}$),
∴${k}_{QP}=\frac{{y}_{0}}{{x}_{0}}$,${k}_{PN}=\frac{\frac{{{y}_{0}}^{3}}{2{{x}_{0}}^{2}+{{y}_{0}}^{2}}-{y}_{0}}{\frac{2{{x}_{0}}^{3}+3{x}_{0}{{y}_{0}}^{2}}{2{{x}_{0}}^{2}+{{y}_{0}}^{2}}-{x}_{0}}=-\frac{{x}_{0}}{{y}_{0}}$,
∴kQP•kPN=-1,则∠QPN=90°.
点评 本题考查了椭圆的标准方程及其性质,训练了直线垂直和斜率间的关系,考查计算能力,是中档题.

| A. | 6e2-6 | B. | 3e2-3 | C. | ex-1 | D. | e2-1 |