题目内容
【题目】已知函数![]() .
.
(1)函数![]() 在
在![]() 处的切线
处的切线![]() 过点
过点![]() ,求
,求![]() 的方程;
的方程;
(2)若![]() 且函数
且函数![]() 有两个零点,求
有两个零点,求![]() 的最小值.
的最小值.
【答案】(1)![]() 即
即![]() ;(2)8.
;(2)8.
【解析】
(1)首先求出在![]() 处的切线方程,然后代入点
处的切线方程,然后代入点![]() ,求参数
,求参数![]() 的值;
的值;
(2)首先利用导数判断函数的单调性和最小值,因为![]() 有两个零点,所以
有两个零点,所以![]() 即
即![]() 得
得![]() ,再根据零点存在性定理证明
,再根据零点存在性定理证明![]() 在
在![]() 上有一个零点,在
上有一个零点,在![]() 上有一个零点,得到
上有一个零点,得到![]() 的最小值.
的最小值.
(1)因为![]() ,
,
所以![]() ,
,
所以![]() 又
又![]() ,
,
所以![]() 在
在![]() 处切线
处切线![]() 方程为
方程为![]() ,
,
即![]() .
.
又因为直线![]() 过点
过点![]() ,所以得
,所以得![]() 即
即![]() .
.
所以直线![]() 方程为
方程为![]() 即
即![]() .
.
(2)因为![]() .
.
令![]() 得
得![]() 即
即![]() ,
,
因为![]() 所以
所以![]() ,
,
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
则![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() .
.
因为![]() 有两个零点,所以
有两个零点,所以![]() 即
即![]() 得
得![]() ,
,
又因为![]() ,
,
![]()
![]() .
.
设![]()
则![]() ,因为
,因为![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
所以![]() .
.
又![]() ,所以
,所以![]() ,
,
故![]() 在
在![]() 上有一个零点,在
上有一个零点,在![]() 上有一个零点,
上有一个零点,
即![]() 在
在![]() 上有两个零点,
上有两个零点,
则![]() 又
又![]() 且
且![]() ,
,
所以![]() 得最小值为8.
得最小值为8.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案【题目】近年来,随着网络的普及,数码产品早已走进千家万户的生活,为了节约资源,促进资源循环利用,折旧产品回收行业得到迅猛发展,电脑使用时间越长,回收价值越低,某二手电脑交易市场对2018年回收的折旧电脑交易前使用的时间进行了统计,得到如图所示的频率分布直方图,在如图对时间使用的分组中,将使用时间落入各组的频率视为概率.
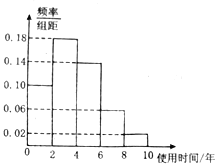
(1)若在该市场随机选取1个2018年成交的二手电脑,求其使用时间在![]() 上的概率;
上的概率;
(2)根据电脑交易市场往年的数据,得到如图所示的散点图及一些统计量的值,其中![]() (单位:年)表示折旧电脑的使用时间,
(单位:年)表示折旧电脑的使用时间,![]() (单位:百元)表示相应的折旧电脑的平均交易价格.
(单位:百元)表示相应的折旧电脑的平均交易价格.
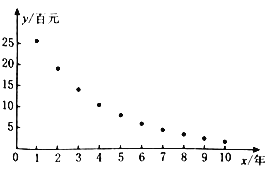
由散点图判断,可采用![]() 作为该交易市场折旧电脑平均交易价格与使用年限
作为该交易市场折旧电脑平均交易价格与使用年限![]() 的回归方程,若
的回归方程,若![]() ,
,![]() ,选用如下参考数据,求
,选用如下参考数据,求![]() 关于
关于![]() 的回归方程,并预测在区间
的回归方程,并预测在区间![]() (用时间组的区间中点值代表该组的值)上折旧电脑的价格.
(用时间组的区间中点值代表该组的值)上折旧电脑的价格.
|
|
|
|
|
|
5.5 | 8.5 | 1.9 | 301.4 | 79.75 | 385 |
附:参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: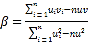 ,
,![]() .参考数据:
.参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.