题目内容
已知正项等比数列{an}的公比为q，其前n项和为Sn，若对一切n∈N*都有an+1≥2Sn，则q的取值范围是 ．
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：由an+1≥2Sn，可得Sn+1≥3Sn，即qn（q-3）+2≥0，利用q＞0，即可确定q的取值范围．
解答：
解：∵an+1≥2Sn，
∴Sn+1≥3Sn，
∴1-qn+1≥3（1-qn），
∴qn（q-3）+2≥0，
∵q＞0，
∴q≥3
故答案为：[3，+∞）．
∴Sn+1≥3Sn，
∴1-qn+1≥3（1-qn），
∴qn（q-3）+2≥0，
∵q＞0，
∴q≥3
故答案为：[3，+∞）．
点评：本题考查q的取值范围，考查等比数列的求和公式，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
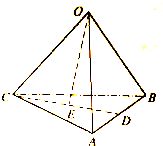如图，在棱长均相等的四面体O-ABCD中，D为AB的中点，E为CD的中点，设| OA |
| a |
| OB |
| b |
| OC |
| c |
| OE |
| a |
| b |
| c |
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
函数f（x）=（x+1）|log2x|-1的零点个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
若2°的圆心角所对的弧长为2m，那么这个弧所在圆的面积为（ ）
A、
| ||
B、
| ||
C、（
| ||
D、
|