题目内容
已知矩形ABCD的周长为l，面积为a．
（1）当l=4时，求面积a的最大值；
（2）当a=4时，求周长l的最小值．
解：（1）设矩形ABCD的长为x，则宽为2-x（0＜x＜2）
∴a=x（2-x）=-（x-1）2+1
∴当x=1时，a有最大值1
（2）设矩形ABCD的长为x，则宽为
（x＞0）
∴
=8
当且仅当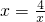
，即x=2时，l有最小值8
分析：（1）设出矩形的长与宽，表示出面积，利用配方法，可得结论；
（2）设出矩形的长与宽，表示出周长，利用基本不等式，可得结论．
点评：本题考查函数的最值，考查配方法、基本不等式的运用，考查学生的计算能力，属于中档题．
∴a=x（2-x）=-（x-1）2+1
∴当x=1时，a有最大值1
（2）设矩形ABCD的长为x，则宽为
（x＞0）∴
=8 当且仅当
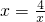，即x=2时，l有最小值8 分析：（1）设出矩形的长与宽，表示出面积，利用配方法，可得结论；
（2）设出矩形的长与宽，表示出周长，利用基本不等式，可得结论．
点评：本题考查函数的最值，考查配方法、基本不等式的运用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
18、如图，已知ABCD是矩形，E是以CD为直径的半圆周上一点，且平面CDE⊥平面ABCD，求证：CE⊥平面ADE．
