Question

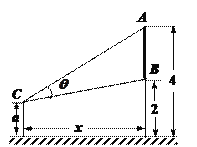
【题目】如图，墙上有一壁画，最高点离地面4米，最低点离地面2米，观察者从距离墙米，离地面高米的处观赏该壁画，设观赏视角

（1）若问：观察者离墙多远时，视角最大？

（2）若当变化时，求的取值范围.

Answer 1

【答案】（1）当观察者离墙米时，视角最大；（2）

【解析】试题分析：（1）利用两角差的正切公式建立函数关系式，根据基本不等式求最值，最后根据正切函数单调性确定最大时取法，（2）利用两角差的正切公式建立等量关系式，进行参变分离得，再根据a的范围确定范围，最后解不等式得的取值范围.

试题解析：（1）当时，过作的垂线，垂足为，

则，且，

由已知观察者离墙米，且，

则，

所以， ，

当且仅当时，取“”．

又因为在上单调增，所以，当观察者离墙米时，视角最大．

（2）由题意得，，又，

所以，

所以，

当时，，所以，

即，解得或，

又因为，所以，

所以的取值范围为．