题目内容
【题目】某调查机构随机调查了![]() 岁到
岁到![]() 岁之间的
岁之间的![]() 位网上购物者的年龄分布情况,并将所得数据按照
位网上购物者的年龄分布情况,并将所得数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成
分成![]() 组,绘制成频率分布直方图(如图).
组,绘制成频率分布直方图(如图).
(1)求频率分布直方图中实数![]() 的值及这
的值及这![]() 位网上购物者中年龄在
位网上购物者中年龄在![]() 内的人数;
内的人数;
(2)现采用分层抽样的方法从参与调查的![]() 位网上购物者中随机抽取
位网上购物者中随机抽取![]() 人,再从这
人,再从这![]() 人中任选
人中任选![]() 人,设这
人,设这![]() 人中年龄在
人中年龄在![]() 内的人数为
内的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.

【答案】(1)192;(2)![]()
【解析】试题分析:(1)根据所有小长方形面积和为1,解得![]() ,再根据频数等于频率与总数的乘积得年龄在
,再根据频数等于频率与总数的乘积得年龄在![]() 内的人数;(2)先根据分层抽样确定各区间抽取人数,再确定随机变量确定,利用组合数求对应概率,列表可得分布列,最后根据数学期望公式求期望.
内的人数;(2)先根据分层抽样确定各区间抽取人数,再确定随机变量确定,利用组合数求对应概率,列表可得分布列,最后根据数学期望公式求期望.
试题解析:(1)由频率分布直方图,可得![]() ,得
,得![]() .
.
则这![]() 位网上购物者中年龄在
位网上购物者中年龄在![]() 内的频率为
内的频率为![]() ,
,
故这![]() 位网上购物者中年龄在
位网上购物者中年龄在![]() 内的人数为
内的人数为![]() .
.
(2)由频率分布直方图可知,年龄在![]() 内的人数与其他年龄段的总人数比为
内的人数与其他年龄段的总人数比为![]() ,
,
由分层抽样的知识知,抽出的![]() 人中年龄在
人中年龄在![]() 内的人数为
内的人数为![]() ,其他年龄段的总人数为
,其他年龄段的总人数为![]() .
.
所以![]() 的可能取值为
的可能取值为![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]()
所以![]() 的分布列为
的分布列为
| 0 | 1 | 2 |
|
|
|
|
故![]() 的数学期望
的数学期望![]() .
.

 亮点激活精编提优100分大试卷系列答案
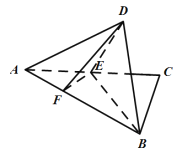
亮点激活精编提优100分大试卷系列答案【题目】直角三角形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上一个动点,且
上一个动点,且![]() ,如图所示,沿
,如图所示,沿![]() 将
将![]() 翻折至
翻折至![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.
(1)当![]() 时,证明:
时,证明:![]() 平面
平面![]() ;
;
(2)是否存在![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角的正弦值是
所成的角的正弦值是![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【题目】【2018四川南充高三第二次(3月)高考适应性考试】某校开展“翻转合作学习法”教学试验,经过一年的实践后,对“翻转班”和“对照班”的全部220名学生的数学学习情况进行测试,按照大于或等于120分为“成绩优秀”,120分以下为“成绩一般”统计,得到如下的![]() 列联表:
列联表:
成绩优秀 | 成绩一般 | 合计 | |
对照班 | 20 | 90 | 110 |
翻转班 | 40 | 70 | 110 |
合计 | 60 | 160 | 220 |
(I)根据上面的列联表判断,能否在犯错误的概率不超过0.001的前提下认为“成绩优秀与翻转合作学习法”有关;
(II)为了交流学习方法,从这次测试数学成绩优秀的学生中,用分层抽样方法抽出6名学生,再从这6名学生中抽3名出来交流学习方法,求至少抽到1名“对照班”学生交流的概率.
附表:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |