题目内容
18.不等式组$\left\{\begin{array}{l}{y≥-1}\\{x+y≤4}\\{5x-3y≥0}\end{array}\right.$表示的平面区域的面积是7.分析 先作出不等式组对应的平面区域,然后根据区域确定面积即可.
解答 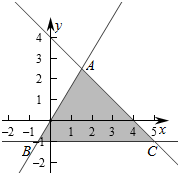 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
由$\left\{\begin{array}{l}{y=-1}\\{x+y=4}\end{array}\right.$得$\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$.即C(5,-1),
由$\left\{\begin{array}{l}{y=-1}\\{5x-3y=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=-\frac{3}{5}}\\{y=-1}\end{array}\right.$,即B($-\frac{3}{5}$,-1),
由$\left\{\begin{array}{l}{x+y=4}\\{5x-3y=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=\frac{5}{2}}\end{array}\right.$,即A($\frac{3}{2}$,$\frac{5}{2}$),
在△ABC的面积S=$\frac{1}{2}$(5+$\frac{3}{5}$)×$\frac{5}{2}$=7,
故答案为:7.
点评 本题主要考查不等式组表示的平面区域,利用二元一次不等式组表示平面区域,作出不等式组对应的区域是解决本题的关键,然后根据相应的面积公式进行求解.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
8.在等差数列{an}中,若a1+a2+a3=32,a11+a12+a13=118,则a4+a10=( )
| A. | 45 | B. | 50 | C. | 75 | D. | 60 |
3.函数f(x)=asinx-bcosx,若f($\frac{π}{4}$+x)=-f($\frac{π}{4}$-x),则函数y=f($\frac{3π}{4}$-2x)的一条对称轴方程是( )
| A. | x=$\frac{π}{6}$ | B. | x=$\frac{π}{4}$ | C. | x=-$\frac{3π}{2}$ | D. | x=-$\frac{2π}{3}$ |