题目内容
7.已知0<x<2.5,则函数y=x2(5-2x)的最大值为$\frac{125}{27}$.分析 由题意可得y=x2(5-2x)=x•x(5-2x)≤($\frac{x+x+5-2x}{3}$)3,注意等号成立的条件即可.
解答 解:∵0<x<2.5,
∴y=x2(5-2x)=x•x(5-2x)
≤($\frac{x+x+5-2x}{3}$)3=$\frac{125}{27}$
当且仅当x=5-2x即x=$\frac{5}{3}$时取等号,
故答案为:$\frac{125}{27}$.
点评 本题考查基本不等式求最值,属基础题.

练习册系列答案
相关题目
16.函数y=|x+1|+1的图象是( )
| A. | 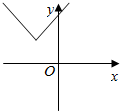 | B. |  | C. | 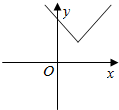 | D. |  |